Example-1) . Check whether the given pair of equations represent intersecting, parallel or coincident lines. Find the solution if the equations are consistent.
2x + y -5 = 0
3x -2y -4 = 0
sol) a1 = 2 b1 = 1 c1 = -5
a2 3 b2 -2 c2 -4
Since a1 =/= b1
a2 b2,
.^. they are intersecting lines and hence, consistent pair of linear equation.
The unique solution of this pair of equations is (2,1)
****************************************
Example 2)Check whether following pair of equation is consistent.
3x + 4y -2 = 0
6x + 8y -4 = 0
Verify by a graphical representation.
sol) (a1/a2) = (3/6) = (1/2)
=> (b1/b2) = (4/8) = (1/2)
=>(c1/c2) = (-2/-4) = (1/2)
Since
a1 = b1 = c1
a2 b2 c2
.^. they are coincident lines.So, the pair of linear equations is dependent and have infinitely many solutions.
Graph:-
Example 3) Check whether the equations are consistent. Also verify by graphical representation
2x-3y =5
4x-6y=15
sol) 2x -3y -5 = 0 & 4x-6y-15=0
a1 = 4 = 2
a2 2 1
b1 = -6 = 2
b2 -3 1
c1 = -15 = 3
c3 -5
a1 = b1 =/= c1
a2 b2 c3
So the equation are inconsistent. They have no solutions and its graph if of parallel lines
(*)Graph:-
****************************************
Example 4) In a garden there are some bees and flowers. If one bee sits on each flower then one bee will be left. If two bees sit on each flower, one flower will be left. Find the number of bees and number of flowers.
sol) Let the no.of bees = x
let the no.of flower = y
If one bee sits on each flower then one bee will be left.
So, x =1( y+1)
or
x-y-1=0----------(1)
If two bees sit on each flower, one flower will be left.
so, x = 2(y-1)
=> x -2y +2 = 0-----(2)
(*)Graph:-
.^., there are 4 bees and 3 flowers
*****************************************
Example 5) The perimeter of a rectangular plot is 32m. if the length is increased by 2m and the breadth is decreased by 1m, the area of the plot remains the same. Find the length and breadth of the plot.
sol) let length and breadth of the rectangular land be "L" and "B" respectively . Then,
area = L * B and
perimeter = 2(l + b) = 32m
l + b =
2
l + b = 16
or
l + b - 16 = 0 ----(1)
When length is increased by "2m", then new length is "L+2". Also breadth is decreased by "1m" so new breadth is "b-1".
Then, area = (L +2) * (b -L)
Since there is no change in the area.
(L+2)(b-L) = Lb
-L +2b -2 = 0
L - 2b -2 = 0 ------(2)
(*) Graph:-
***************************************
Exercise - 4.1
1) By comparing the ratios
a1, b1, c1,
a2 b2 c2
find out whether the lines represented by the following pairs of linear equations intersect at a point, are parallel or are coincident.
(a) 5x - 4y + 8 = 0
7x + 6y - 9 = 0
sol) 1) 5x -4y +8 =0 comparing with a1x + b1y + c = 0
Where a1 =5, b1= -4, c1=8
2) 7x +6y -9 =0 comparing with a2x + b2y + c2=0
Where a2 = 7, b2= 6, c2= -9
a1 = 5
a2 7
= b1 = -4 = -2
b2 6 3
= c1 = 8 = - 8
c2 -9 9
Since a1
a2 b2
Thus, we have a unique solution
.^. , the lines that represent the linear equations intersect at a point.
-------------------------------------------------------------------------------------
b) 9x + 3y + 12 = 0
18x + 6y +24 =0
sol)
1) 9x + 3y +12 comparing with a1x + b1y + c1 = 0
Where a1 = 9, b1 = 3, c1 = 12
2) 18x + 6y + 24 comparing with a2x + b2y +c2 = 0
Where a2 = 18, b2=6, c2=24
= a1 = 9 = 1
a2 18 2
= b1 = 3 = 1
b2 6 2
= c1 = 12 = 1
c2 24 2
Since a1 ,= b1 =, c1
a2 b2 c2
.^. they are coincident lines.
So, the pair of linear equations is dependent and have infinitely many solutions.
-------------------------------------------------------------------------------------------------
c) 6x - 3y +10 = 0
2x - y + 9 = 0
sol)
1) 6x -3y +10 = 0 comparing with a1x + b1y +c1 = 0
where a1 = 6, b1= -3, c1 = 10
2) 2x -y + 9 = 0 comparing with a2x +b2y +c2 = 0
where a2 = 2, b2= -1, c2 =9
= a1 = 6 = 3
a2 2
= b1 = -3 = 3
b2 -1
= c1 = 10
c2 9
Since a1 = b1 =/= c1
a2 b2 c2
So the equations are inconsistent.
They have no solutions and the lines represent the linear equations are parallel.
*****************************************************************
2) Check whether the following equations are consistent or inconsistent. Solve them graphically
a) 3x + 2y = 5
2x - 3y = 7
sol) 3x + 2y =5 rearranging we get,
3x +2y -5 = 0 comparing with a1x +b1y+ c1= 0\
where a1= 3, b1= 2, c1= -5
2) 2x -3y = 7 Rearranging we get,
2x - 3y - 7 = 0 comparing with a2x +b2y + c2 = 0
where a2 = 2, b2= -3. c2 = -7
= a1 = 3
a2 2
= b1 = 2
b2 -3
= c1 = -5
c2 -7
Since a1 =/= b1 =/= c1
a2 b2 c2
.^. they are intersecting lines and
Hence, consistent pair of linear equation.
Note :- for ( 0, 5/2) = (0, 2.5 ).....( 2, -1/2 ) = ( 2, -0.5),.....
(0, -7/5) = (0 , -1.4)......(2, -3/5) = ( 2, -0.6 ),.... (3, -1/5) = ( 3, - 0.2)
fotGraph :-
****************************************************************************
b) 2x - 3y = 8
4x - 6y = 9
sol) 2x - 3y = 8 , rearranging we get
2x - 3y - 8 = 0 comparing with a1x + b1y +c1 = 0
where a1= 2, b1= -3, c1= -8
2) 4x -6y = 9, rearranging we get
4x-6y-9=0 comparing with a2x +b2y +c2 =0
where a2= 4, b2=-6, c2=-9
= a1 = 2 = 1
a2 4 2
= b1 = - 3 = 1
b2 -6 2
= c1 = -8
c2 -9
a1 = b1 =/= c1
a2 b2 c2
So the equations are inconsistent. They have no solutions and
Its graph is of parallel lines.
Graph :-
*******************************************************************
c) 3x + 5 y = 7
2 3
9x - 10y = 14
sol ) 3x + 5 y -7 =0 { a1x +b1y+c1 = 0)
2 3
where a1 = 3/2, b1 = 5/3, c1= -7
*) 9x - 10y -14 = 0 ( a2x +b2y+c2=0)
Where a2= 9, b2= -10, c2= -14
=> a1 = 3/2
a2 9
=> a1 =
a2 2
=> a1 = 1
a2 6
=> b1 = 5/3
b2 -10
=> b1 =
b2 3
=> b1 = -1
b2 6
=> c1 = -7 = 1
c2 -14 2
Since a1 =/= b1 =/= c1
a2 b2 c2
.^. they are intersecting lines and hence, consistent pair of linear equation.
y = [7 - 3 ] * 3 = 7 *3 - 3 * 3 = 21 -9 x
GRAPH :-
*********************************************************************************
d) 5x -3y = 11
-10x +6y = -22
sol) 5x -3y -11 =0 (a1x +b1y +c1 = 0)
where a1= 5,...b2= -3,....c1= -11
*)10x +6y +22 = 0 ( a2x +b2y+c2 = 0)
Where a2= -10, ...b2=6,....c2= 22
= a1 / a2 = 5 / -10 = 1/ -2
= b1 / b2 = -3 / 6 = -1/2
=> c1 / c2 = 11 / -22 = 1 / -2
Since a1/a2 = b1 / b2 = c1 / c2,
.^. they are coincident lines. So the pair of linear equations is dependent and have infinitely many solutions.
GRAPH :-
******************************************************************
(e)
4 / 3 x + 2y = 8
2x + 3y = 12
sol) 4 / 3x + 2y - 8 = 0 compare with a1x + b1y +c1 = 0
where a1 = 4 / 3 , b1 = 2, c1 = -8
*) 2x + 3y - 12 = 0 compare with a2x + b2y +c2= 0
where a2 = 2, b2= 3, c2= -12
=> a1 / a2 = 4/3 / 2 =
=> b1 / b2 = 2 / 3
=> c1 / c2 = 8 / 12 = 2 / 3
Since a1/a2 = b1 / b2 = c1 / c2,
.^. they are coincident lines. So the pair of linear equations is dependent and have infinitely many solutions.
Graph :-
****************************************************************
(f)
x + y = 5
2x + 2y = 10
Sol) x + y - 5 = 0 { a1x +b1y +c1 }
where a1= 1 , b1= 1, c1= -5
*) 2x + 2y - 10 = 0 { a2x +b2y+c2}
where a2 = 2, b2= 2, c2 = -10
=> a1 / a2 = 1/2
=> b1 / b2 = 1 /2
=> c1 / c2 = -5 / -10 = 1 /2
a1 / a2 = b1 / b2 = c1 / c2
.^. they are coincident lines. So the pair of linear equations is dependent and have infinitely many solutions.
GRAPH:-
***************************************************************************
(g)
*) x - y = 8
3x - 3y = 16
Sol) x-y-8 = 0 { a1x + b1y+c1}
where a1 = 1, b = -1, c1 = -8
3x - 3y - 16 = 0 { a2x + b2y +c2}
where a2 = 3, b2= -3, c2 = -16
=> a1 / a2 = 1 / 3
=> b1 / b2 = -1 / -3 = 1 / 3
=> c1 / c2 = -8 / -16 = 1 /2
Since a1 / a2 = b1 / b2 =/= c1 / c2
So the equations are inconsistent.
They have no solution and its graph is of parallel lines.
GRAPH :-
**************************************************************************
(h)
*) 2x + y - 6 = 0
4x - 2y - 4 = 0
sol) 2x + y - 6 = 0 { a1x + b1y+c1}
where a1 = 2, b1 = 1, c1= -6
*) 4x - 2y - 4 = 0 { a2x + b2y +c2}
where a2= 4, b2= -2, c2= -4
=> a1 / a2 = 2 / 4 = 1 /2
=> b1 / b2 == 1 / -2
=> c1 / c2 = -6 / -4 = 3 /2
Since a1 / a2 =/= b1 / b2=/= c1 / c2
.^. they are intersecting lines and,
Hence, consistent pair of linear equation.
GRAPH :-
************************************************************************
(i) 2x - 2y - 2 = 0
4x - 4y - 5 = 0
sol) 2x - 2y - 2 = 0 { a1x + b1y + c1}
where a1 = 2, b1 = -2, c1 = -2
*) 4x -4y - 5 = 0 { a2x + b2y+c2}
where a2 = 4, b2 = -4, c2 = -5
= > a1 / a2 = 2 / 4 = 1 / 2
=> b1 / b2 = -2 / -4 = 1 / 2
=> c1 / c2 = -2 / -5 = 2 / 5
Since a1 / a2 = b1 / b2 =/= c1 / c2
So the equations are inconsistent.
They have no solution and its graph is of parallel lines.
GRAPH :-
*******************************************************************
3) Neha went to a "sale" to purchase some pants and skirts. When her friend asked her how many of each she had bought, she answered
" The number of skirts are two less than twice the number of pants purchased. Also the number of skirts is four less than four times the number of pants purchased. "
Help her friend to find how many pants and skirts Neha bought.
sol) Let
1) No of pants purchased by Neha be= 'X'
2) No. of skirts purchased by Neha be='Y'
*) The Number of skirts are two less than twice the number of pants = 2x -2
i.e, y ( skirts) = 2x ( twice no. of pants) - 2
y = 2x - 2 ----------- (1)
*) The No. of skirts are four less than four times the no.of pants = 4x - 4
i.e, y =( skirts) = 4x ( fourtime pants) - 4
y = 4x - 4------------- (2)
Subtracting 1) from (2) we get,
y = 4x - 4
y = 2x - 2
2x- 2
2x -2 = 0
2x = 2
x = 1 -------- (3)
Substitute (3) in either (1) or (2) we get 'y' value
y = 2 (1) - 2
= 2 -2
y = 0
.^. No of pants purchased = 1
No of skirts purchased = 0
*****************************************************************
4) 10 students of class-X took part in mathematics quiz. if the number of girls is 4 more than the number of boy's then, find the number of boys and number of girls who took part in the quiz.
sol) Let the no. of boys be = X
Let the no. of girls be = Y
Total no. of students ( X + Y ) = 10
Condition :- if the no.of girls (y) is 4 more than the no. of. boys (x)
i.e, y = 4 + X
X + Y = 10 ------- (1)
y = 4 + X ----- (2)
Substitute (2) in (1) we get
X + 4 + X = 10
2x + 4 = 10
2x = 10 - 4
2x = 6
x = 6 / 2
x = 3 -------- (3)
Substitute 'x= 3" in either (1) or (2) we get
when x = 3
y = 4 +x
y = 4 + 3
y = 7
.^, there are x = 3 (boys) and y = 7 (girls) in the class.
**************************************************************
5) 5 pencils and 7 pens together cost 50R whereas 7 pencils and 5 pens together cost 46R. Find the cost of one pencil and that of one pen
sol) Let the cost of one pencil be = X
Let the cost of one pen be = Y
Condition 1 :- 5 pencils(x) and 7 pens(y) cost 50R
i.e, 5x + 7y = 50
Condition 2 :- 7 pencils(x) and 5 pens(y) cost 46R
i.e, 7x + 5y = 46
we got two equations
5x + 7y = 50 --------------------- (1)
7x + 5y = 46 -------------------(2)
try to eliminate either "x" or "y" value by multiplying both equations with any number
Lets multiply (1) with 7 and (2) with 5
7 *( 5x + 7y -50) = 35x + 49y - 350
5 * ( 7x + 5y - 46) = 35x + 25y - 230
we got
35x + 49y = 350 ----- ---(3)
35x +25y = 230 --------(4)
subtracting (3) and (4)
35x +49y = 350
35x + 25y = 230
- - -
24y = 120
=> 24y = 120
=> y = 120 / 24 = 5 ( 24 *5 = 120)
we got y = 5 , substitute in any (1) or (2) equation
=> 5x + 7y = 50
=> 5x + 7 ( 5 ) = 50
= > 5x + 35 = 50
=> 5x = 50 - 35
=> 5x = 15
= > x = 15 / 5
=> x = 3
Hence we got x = 3 ( 1 pencils cost ) and y = 5 ( 1 pens cost)
********************************************************
6) Half the perimeter of a rectangular garden, whose length is 4m more than its width, is 36m.Find the dimensions of the garden.
sol) Let the length and width of the rectangular garden be "l" and ' b" respectively .
We know perimeter of rectangle is = 2 ( l +b)
condition :- Half the perimeter ( 1/ 2) of a rectangular garden , whose length is 4m more than its width ( 4 +b) is 36m
Half the perimeter ( 1 ) *
=> l +b = 36 ------ (1)
Given :- l = 4 +b ( 4m more than width )...--- (2)
substitute (2) in (1)
=> (4 + b) + b = 36
=> 4 + 2b = 36
=> 2b = 36 - 4
=> 2b = 32
=> b = 16
substitute b = 16 in (1) or (2)
=> l = 4 +b
=> l = 4 + 16
=> l = 20
Hence , the length of the garden is 20m and its width is 16m
**************************************************************
7) We have a linear equation 2x +3y -8 = 0, . Write another linear equation in two variables such that the geometrical representation of the pair so formed is intersecting lines.
Now, write two more linear equations so that one forms a pair of parallel lines
and the 2nd form coincident line with the given equation.
sol) 1) pair forming intersecting lines :-
1st equation :- 2x + 3y - 8 = 0 comparing with a1x +b1y +c1 = 0
where a1 = 2 , b1 = 3 , c1 = -8
Let 2nd equation be ax +bx +c = 0 comparing with a2x + b2y + c2 = 0
where a2 = a , b2 = b , c2 = c
We know for intersecting lines one condition should be satisfied
i.e, a1 =/= b1
a2 b2 --------------- (1)
=> a1 / a2 = 2 / a
=> b1 / b2 = 3 / b
Hence 2/ a =/= 3 / b--------(2)
take "a" and "b" value in such a way that condition (1) should be satisfied
lets assume a = 5 and b = 4 and c = 7
then 2nd equation will become = 5x + 4y + 7
substitute a and b value in (2) we get
=> 2 / 5 =/= 3 / 4
.^. the equation is satisfied. a1 / a2 =/ = b1 / b2
***********************************************************************
2) pair forming parallel lines :-
For two equations to be parallel one condition should be satisfied
i.e, a1 / a2 = b1 / b2 =/= c1 /c2 ------- (1)
1st equation :- 2x + 3y - 8 = 0 ( a1x + b1y + c1)
where a1 = 2, b1 = 3 , c1 = -8
Let the 2nd equation be ax +by +c = 0 (a2x +b2y+c2)
where a2 = a, b2 = b, c2 = c
Take a, b,c value in such a way that condition (1) should be satisfied.
let a = 2, b = 3, c = 5
then a2 = 2, b2 = 3 and c2 = 5
Now
=> a1 / a2 = 2 / 2 = 1
=> b1 / b2 = 3 / 3 = 1
=> c1 / c2 = -8 / 5
Since a1 / a2 = b1 / b2 =/= c1 / c2
.^. Hence pair of lines are parallel
****************************************************************
3) Pair forming coincident lines :-
For pair of two equations to be coincident one condition should be satisfied.
i.e, a1 / a2 = b1 / b2 = c1 / c2----------- (1)
1st equation :- 2x +3y - 8 = 0 { a1x +b1y +c1}
where a1 = 2, b1 = 3, c1 = -8
Let the 2nd equation be ax +by +c = 0 ( a2x +b2y +c2)
where a2 = a, b2 = b, c2 = c
=> a1 / a2 = 2 / a
=> b1 / b2 = 3 / b
=> c1 / c2 = -8 / c
since 2 /a = 3 / b = -8 / c ------- (2)
take a,b,c value in such a way that (1) condition should be met.
let a = 6 , b = 18 , c = -24
then 2nd equation becomes
6x + 18y - 24 = 0
now (2) condition becomes
=> 2 / 6 = 1 / 3
=> 3 / 18 = 1 / 3
=> -8 / - 24 = 1 / 3
Hence a1 / a2 = b1 / b2 = c1 /c2
.^. the pair of lines are coincident
*********************************************************
8) The area of rectangle gets reduced by 80 units if its length is reduced by 5 units and breadth is increased by 2 units. If we increase the length by 10 unites and decrease the breadth by 5 units, the area will increase by 50 sq units. Find the length and breadth of the rectangle.
sol) Let area of rectangle be = 'A"
let length be = L
let breadth be = b
we know Area of rectangle =( L * B )
i.e, Formula : A = l * b ------ (1)
1st condition :- Area get reduced by 80 units, length reduced by 5 units and breadth increased by 2 units
Given ;-
=> (A - 80) [ Area reduced by 80 ] ------ (2)
=> ( L- 5) [ length reduced by 5 ] ---------(3)
=> (b + 2 ) [ Breadth increased by 2 units] ----- (4)
substitute (2) , (3), (4) in (1) we get
A = L * b
( A - 80) = (L-5) (b +2)
(A - 80) = L ( b+2) -5 (b +2)
(A - 80) = Lb + 2L - 5b - 10
A = Lb + 2L -5b - 10 +80
A = Lb + 2L - 5b + 70
in place of A we can write L *b
2L - 5b + 70 = 0
2L - 5b = -70 ------------------------------ (5)
2nd condition ;- Length increase by 10 units , breath decreased by 5 units and area will increase by 50 units
given :-
(A + 50 ) [ area increase by 50 ] -------- (6)
(L + 10) [ length increase by 10 ] ------(7)
(b - 5) [ breadth decreased by 5 ] ------- (8)
now A = L * b
(A + 50 ) = ( L + 10) ( b - 5)
( A + 50 ) = L (b-5) + 10 ( b - 5)
( A + 50 ) = Lb - 5 L + 10b - 50
Lb + 50 = Lb -5L + 10b - 50
-5L + 10b -100 = 0
-5L + 10b = 100 ------------------------ (9)
we got two equation
2L - 5b = - 70
- 5L + 10b = 100
Try to eliminate either "L" or "b" value by multiplying with any number
Lets try to eliminate "L" value so that we get "b"
5 * ( 2L - 5b = - 70 ) = > 10 L - 25b = - 350 -------- (10)
2 * ( -5L +10b = 100) => -10L + 20b = 200 --------- (11)
we got
10L - 25b = -350
-10L + 20b = 200
0 -5b = - 150
-5b = -150
b = -150 / -5
b = 30
substitute "b" value in either (5) or (9) we get "L" value
=> 2L - 5b = -70
=> 2L - 5(30) = -70
=> 2L - 150 = -70
=> 2L = 150 -70
=> 2L = 80
=> L = 80 / 2
=> L = 40
.^. we got L= 40 and b = 30
*********************************************************************
9) in X class, if three students sit on each bench, one student will be left. If four students sit on each bench, one bench will be left. Find the number of students and the number of benches in that class
sol) Let no.of students = X
Let no. of benches = Y
condition :- if 3 students(x) sit on each bench(y), one student will be left
total no.of students (x) = 3y +1
i.e, x = 3y +1 ------------(1)
2nd condition :- if 4 students sit on each bench, one bench will be left
total no of students (x) = 4 (y-1)
i.e, x = 4y - 4------ (2)
equating (1) and (2) we get
3y +1 = 4y - 4
1 +4 = 4y -3y
5 = y ( no of benches)
substitute "y" value in (1) or (2) we get
x = 3y +1
x = 3(5) +1
x = 15 +1
x = 16
.^. there are 16 students and 5 benches.
*****************************************************************
Exercise - 4.2
(*) Substitution Method:-
Example 1): Solve the given pair of equations using substitution method.
2x - y = 5 -----------(1)
3x +2y = 11 ---------(2)
sol) Eq(1) can be written as
y = 2x - 5 -----(step 1)
substitute (step 1) in eq(2) we get
3x + 2(2x-5) = 11 ------(step 2)
3x + 4x - 10 = 11
x = 3----------(step 3)
substitute "x=3" in eq(1) we get,
2(3) - y = 5
y =6-5
y = 1 ---------(step 4)
substitute the values of "x" and "y" in eq(2), we get
3(3) + 2(1)
=> 9 +2
=> 11
Both the equations are satisfied by x=3 and y=1.---(step 5)
.^., required solution is x= 3 and y = 1
********************************************************
(*) Elimination Method:-
Example 1):-Solve the following pair of linear equations using elimination method
3x + 2y = 11 --------(1)
2x + 3y = 4 --------(2)
sol) Let us eliminate "y" from the given equations. The co-efficients of "y" in the given equations are "2" and "3".
L.C.M of "2" and "3" is 6.
So, multiply equation(1) by 3 and equation (2) by 2.
eq(1) * 3 => 9x + 6y = 33
eq(2) *2 => 4x + 6y = 8
(-) (-) (-)
5x = 25
x = 25
5
x = 5
substitute "x=5" in eq(1)
3(5) + 2y = 11
2y = 11-15
y = -4/2
y = -2
.^. , the required solution is X=5, y = -2
******************************************************
Example 2).Tabita went to bank to withdraw 2000rs. She asked cashier to give the cash in 50rs and 100rs notes only. Sandhya got 25 notes in all. can you tell how many notes each of 50rs and 100rs she received?
sol) Let the number of 50rs notes = x
Let the number of 100rs notes = y
then, x +y = 25 ------(1)
and 50x + 100y = 2000 -----(2)
Kavitha used the substitution method
From eq(1) => x = 25-y
substitution "x=25 -y" in eq(2)
we get,
50(25-y) + 100y = 2000
1250 - 50y +100y = 2000
50y = 2000-1250
y = 750
50
y = 15
substitute "y=15" in "x=25-y"
we get,
x = 25 - 15
x = 10
Hence, Tabita received ten 50rs notes and fifteen 100rs notes.
sandhya used the elimination method to get the solution.
In the equations, co-efficients of "x =1 and 50 respectively. So,
eq(1) *50 => 50x + 50y = 1250
eq(2) * 1 => 50x +100y =2000 (same sign, so subtract)
(-) (-) (-)
-50y = -750
y = -750
-50
y = 15
substitute "y" in eq(1), we get
x +15 = 25
x = 25-15
x = 10
Hence, sandhya received ten 50rs and fifteen 100rs notes.
******************************************************
Example 3). In a competitive exam, 3 marks are to be awarded for every correct answer and for every wrong answer, one mark will be deducted.Madhu scored 40 marks in this exam.
Had 4 marks been awarded for each correct answer and 2 marks deducted for each incorrect answer, Madhu would have scored 50 marks.
How many questions were there in the test?( Madhu attempted all questions).
sol) Let the number of correct answers =x
Let the number of wrong answers = y
When 3 marks are given for each correct answer and 1 mark deducted for each wrong answer, his score is 40 marks.
3x - y = 40 ------(1)
His score would have been 50 marks if 4 marks were given for each correct answer and 2 marks deducted for each wrong answer.
4x -2y = 50 -------(2)
substitution method
from eq(1) => y = 3x - 40
substitute"y= 3x -40 " in eq(2)
we get,
4x - 2(3x - 40) = 50
4x -6x +80 = 50
-2x = 50 - 80
x = 30
2
x = 15
substitute "x=15" in eq(1)
we get,
3(15) - y = 40
45 - y = 40
y = 45 -40
y = 5
.^. total number of questions = 15+5 = 20
*****************************************************
Example 4). Mary told her daughter, "Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be. " Find the present age or Mary and her daughter.
sol) Let Mary's present age be = x
Her daughter's age be = y
Then, seven years ago Mary's age was "x-7"
daughter age was"y-7"
seven time as old as you:-
x-7 = 7(y-7)
x-7 = 7y -49
x - 7y +42 = 0 --------(1)
Three years hence, Mary's age will be "x+3" and daughter's age will be "y+3"
x +3 = 3(y+3)
x+3 = 3y + 9
x -3y -6 = 0 -------(2)
using Elimination method:-
eq(1) => x -7y = -42
eq(2) => x - 3 = 6
(-) (+) (-)
-4y = -48
y = -48
-4
y = 12
Substitute "y=12" in eq(2)
we get,
x -3(12) -6 = 0
x = 36 + 6
x = 42
.^., Mary's present age is 42 years and her daughter's age is 12 years
*******************************************************
Example 5). A publisher is planning to produce a new textbook. The fixed costs(reviewing, editing, typesetting and so on) are 31.25 rs/book. Besides that, he also spends another 320000rs in producing the book. the wholesale price(the amount received by the publisher) is 43.75rs per book. How many books must the publisher sell to break even, i.e, so that the costs will equal revenues?
sol) The publisher breaks even when costs equal revenues.
Break even point :- the point which corresponds to how much money you have to earn through sales in order to equal the money you spent in production
If "x" represents the number of books printed and sold
If "y" represents the breakeven point, then the cost and revenue equation for the publisher are
(*)Cost equation is given by
=> y = 320000 + 31.25x -----(1)
(*) revenue equation is given by
=> y = 43.75x ----------(2)
using the eq(2) to substitute for "y" in the eq(1), we have
43.75x = 3,20,000 + 31.25x
12.5x = 3,20,000
x = 3,20,000
12.5
x = 25,600
Thus, the publisher will break even when 25,600 books are printed and sold.
******************************************
Form a pair of linear equations for each of the following problems and find their solution.
1) The ratio of incomes of two persons is 9:7 and the ratio of their expenditures is 4:3. If each of them manages to save 2000R per month. Find their monthly income.
sol) Let the monthly incomes be = X
Let monthly expenditures be = Y
Given income ratios of two persons = 9x : 7x
Expenditure ratio of two persons = 4y : 3y
Both of them manage to save rs. 2000/ month
we know that
income - expenditure = savings
Then,
9x - 4y = 2000 --------- (1) person
7x - 3y = 2000 ----------(2) person
Multiply (1) by 3 and (2) by 4 ,we get
3 *( 9x - 4y = 2000 ) = 27x -12y = 6000 ----- (3)
4*( 7x - 3y = 2000) = 28x -12y = 8000 ---- (4)
subtract 3 and 4 we get,
28x -12y = 8000
27x - 12y = 6000
- + -
x 0 = 2000
x = 2000 ------ (5)
substitute (5)in (1)we get
9( 2000) - 4y = 2000
18000 - 2000 = 4y
16000 = 4y
16000 / 4 = y
4000 = y
we got income(x) = 2000, and expenditure (y) = 4000
income of first person
= 9x
= 9 * 2000 = 18000
income of second person
= 7x
= 7 * 2000 = 14000
*******************************************************************
2) The sum of a two digit number and the number obtained by reversing the digits is 66. If the digits of the number differ by 2, find the number. How many such numbers are there?
sol) let the digit in units place be = x
Let the digit in tens place be = y
then, the number formed = 10y +x
The number obtained by reversing the order of the digits = 10x +y
condition :- ssum of 2 digit number is 66
i.e, ( 10y+x) + (10x +y) = 66
=> 10y + x +10x +y = 66
=> 11y + 11x = 66
=> 11 (y+x) = 66
=> x +y = 66 / 11
=> x +y = 6 ----- (1)
2nd condition :- digit differ by "2"
so either x -y = 2 (or) y - x = 2 => -x +y = 2 => x - y = -2
Thus, we have the following sets of simultaneous equations.
=> x + y = 6 ----- (2)
x - y = 2 -------(3)
(or)
=> x + y = 6 ----- (4)
x - y = -2 ----- (5)
solve (2) and (3) we get
x + y = 6
x - y = 2
2x =8
x = 4
substitute "x' in (2)
=> x+ y = 6
=> 4 + y = 6
=> y = 6 -4
=> y = 2
we got x = 4 and y = 2
Also solve (4) and (5) we get
x + y = 6
x - y = -2
2x = 4
x = 2 put in (4) we get
=> x + y = 6
=> 2 +y = 6
=> y = 4
we got x = 2 and y = 4
When x =4 and y= 2. The number formed is :-
=> 10y + x
=> 10 (2) + 4
=> 20 + 4
=>24
when x = 2 and y = 4.. reverse number is
10y + x
=> 10 (4)+ 2
=> 40 + 2
=> 42
Hence the required number is either 24 or 42
**************************************************************
3) The larger of two supplementary angles exceeds the smaller by 18 degree. Find the angles.
sol) Let the larger angle be = Y
Let the smaller angle be = X
given :- larger angle( y) exceed the smaller(x) by 18
i.e, y = x +18 ----- (1)
we know sum of supplementary angles is 180
=> x + y = 180 ---- (2)
put (1) in (2)
=> x + x + 18 = 180
=> 2x = 180 - 18
=> 2x = 162
=> x = 162 / 2
=> x = 81 ------ (3)
substitute (3) in (1)
y = 81 +18
=> y = 99
.^. larger angle = 99 and smaller angle = 81
*********************************************************
4) The taxi charges in Hyderabad are fixed , along with the charge for the distance covered. For a distance of 10 km., the charge paid is 220R . For a journey of 15km the charge paid is 310R
1) What are the fixed charges and charge per km?
2) How much does a person have to pay for travelling a distance of 25 km?
sol) let the fixed charge be= X
Let the charge for the distance covered be = Y
1st condition. ;- Distance 10km, charge paid is 220R
i.e, total charge 220R = fixed charge + charge for distance
220 = x + 10y ----- (1)
2nd condition :- For 15km, the amouth is 310Rs
i.e, x + 15y = 310 ------ (2)
solve (1) and (2) we get,
x + 10y = 220
x + 15y = 310
- - -
-5y = - 90
=> - 5y = - 90
=> y = 90 / 5
=> y = 18 -------- (3)
substitute (3) in (1) we get,
=> x + 10( 18) = 220
=> x+ 180 = 220
=> x = 220 - 180
=> x = 40
1 sol ) fixed charges = 40 and charge / km = 18
2) how much does a person have to pay for travelling a distance of 25 km?
sol) as we got fixed charge = 40 value and charge/km = 18
and we know total charge = fixed charge + charge/ distance
= > x + 25y
=> 40 + 25 (18) = 40 +450 = 490
Hence for 25 km , the taxi charge = 490
*************************************************************
5) A fraction becomes 4 / 5 if 1 is added to both numerator and denominator. If , however, 5 is subtracted from both numerator and denominator, the fraction becomes 1 /2 ... What is the fraction.
sol) Let the numerator be = X
Let the denominator be = Y
Hence the fraction = X / Y
1st condition :- 1 is added to numerator and denominator
x + 1 = 4
y +1 5
=> 5 ( x +1) = 4 (y +1)
=> 5x + 5 = 4y + 4
=> 5x - 4y = 4 - 5
=> 5x - 4y = -1 ------- (1)
2nd condition :- 5 is subtracted from numerator and denominator
x -5 = 1
y - 5 2
2 ( x - 1) = 1 (y -5)
2x - 10=y - 5
2x - y = -5 +10
2x - y = 5----- (2)
Using elimination method:-
multiply (1) by 2
multiply (2) by 5
2 ( 5x - 4y = -1)
=> 10x - 8y = -2 ------ (3)
5 * (2x - y = 5)
=> 10x - 5y = 25 -------- (4)
subtract (3) & (4)
10x - 8y = -2
10x - 5y = 15
- + -
0 -3y = -27
-3y = -27
y = 27 / 3
y = 9
substitute y= 9 value in (1) we get
=> 5x - 4y = -1
=> 5 x - 4(9) = -1
=> 5x - 36 = -1
=> 5x = -1 =36
=> 5x = 35
x = 35 / 5
x = 7
.^. the required fraction is X / y = 7 / 9
*************************************************************
6) Places A and B are 100km apart on a highway. One car starts from A and another from B at the same time at different speeds. If the cars travel in the same direction , they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of the two cars?
sol) Let the speed of 1st car = x km/hr
Let the speed of 2nd car = y km/hr
1st condition :- 1st car starts from A and another from B at same time at different speeds , If both travels in same direction, they meet in 5hrs
<------------100km---------->
A-------------------------------B-----------------L---->
We have formula Distance = time * speed
Distance covered by 1st car in 5hrs = 5 * x km/hr
Distance covered by 2nd car in 5 hrs = 5 * y km/hr
Let "L" is the point where both car meets.
.^. AL = 5x km and
BL - 5y km
.^. Al - BL = AB
=> 5x - 5y = 100
=> 5 (x -y) = 100
=> x - y = 100 / 5
=> x - y = 20 ------------ (1)
2nd condition :- When both car moves in opposite direction they meet in 1 hr
<--------------------------100km--------------->
A----------------------M-----------------B ---->
Distance covered by 1st car in 1hr = 1 * x km
Distance covered by 2nd car in 1 hr = 1 * y km
Let "M" is the point where both meet
.^. AM = 1xkm and BM = 1ykm
.^. AM + BM = AB
=> 1xkm + 1y km = 100
=> x + y = 100 -------- (2)
Adding (1) and (2) we get,
x - y - 20
x + y = 100
2x = 120
2x = 120
x= 120 / 2
x = 60
Substitute x = 60 in (1) , we get
x - y = 20
60 - y = 20
60 - 20 = y
40 = y
.^> Speed of 1st car is 60 km/hr
.^. Speed of 2nd car is 40 km/hr
*****************************************************************
7) Two angles are complementary. The larger angel is 3degree less than twice the measure of the smaller angle. Find the measure of each angle.
sol) Let the smaller angle = x
let the larger angle = y
given :- larger angle is 3deg less than twice the measure of smaller angle.
i.e, y ( larger) = 2x ( twice ) - 3
y = 2x - 3 ----- (1)
Give the two angles are complementary
i.e, x + y = 180 ------ (2)
substitute (1 in (2),, we get
=> x + y = 180
=> x + (2x - 3) = 180
=> x + 2x - 3 = 180
=> 3x - 3 = 180
=> 3x = 180 +3
=> x = 183 / 3
=> x = 61 degree
substitute x = 61 in (1) we get ,
y = 2x - 3
y = 2 (61) - 3
y = 122 - 3
y = 119 degree
Hence ,
Larger angle = 119
Smaller angle = 61
********************************************************
8) An algebra textbook has a total of 1382 pages. It is broken up into two parts. The second part of the book has 64 pages more than the first part.. How many pages are in each part of the book?
Sol) No. of pages in 1st part = X
No. of pages in 2nd part = Y
Given :- total ( x+y ) = 1382
i.e, x +y = 1382 ------- (1)
condition :- 2nd part of the book has 64 more pages
i.e, y = x +64
Substitute y = x +64 in (1) we get,
x + y = 1382
x + x +64 = 1382
2x = 1382 - 64
2x = 1318
x = 659
Substitute x = 659 in y = x +64
y = 659 +64
y = 723
.^. The pages in 1st part = 659
.^. The pages in 2nd part = 723
*********************************************************
9) A chemist has two solutions of hydrochloric acid in stock. One is 50 % solution and the other is 80% solution. How much of each should be used to obtain 100ml of a 68% solution.
sol) Let the proportion of the first solution be represented be= X
Let the proportion of the second solution be
= Y
given :- 1st solution contains 50 % solution =
=
Given together they should give 100 ml of 68% solution .
i.e, x + 4y = 100 * 68%
2 5
x / 2 + 4y / 5 =
2 5
=> 5x + 8y = 68
10
=> 5x + 8y= 68 *10
=> 5x + 8y= 680 --------- (1)
*) Total percentage of solution concentration is 100 %
x + y = 100 ---------- (2)
Multiply equation (1) with "1" and (2) with 5 . we get,
1 * ( 5x + 8y = 680 ) = > 5x + 8y = 680
5 * ( x + y = 100) => 5x + 5y = 500
5x + 8y = 680
5x + 5y = 500
- - -
0 3y = 180
3y = 180
y = 180/ 3
y = 60
substitute y = 60 in eq (2) we get
x + y = 100
x + 60 = 100
x = 100 -60
x = 40
Hence the required solutions are 40ml and 20ml
**********************************************************
10) Suppose you have 12000Rs to invest . You have to invest some amount at 10% and rest at 15%. How much should be invested at each rate to yield 12% on the total amount.
sol) Let the amount to be invested at 10% be = X
Let the amount to be invested at 15% be = Y
Total amount to be invested = 12000 rs
ie., x + y = 12000 ------ (1)
condition :-
Invest some amount at 10% =
invest some amount at 15% =
2nd condition
i.e, 12000( total amount) * 12 %
=> 120
10 20
20 X + 30y = 1440
200
=> 2x + 3y = 1440 20
=> 2x + 3y = 1440 * 20
=> 2x + 3y = 28,800 --------------- (2)
multiply eq.(1) by 2 and solving with eq. (2) we get,
2*( x + y= 12,000)
2x + 2y = 24000 ------- (3)
subtract eq (2) and eq (3)
2x + 3y = 28,800
2x + 2y = 24000
- - -
y = 4800
substitute y = 4800 in (1) we get,
x + y = 12000
x + 4800 = 12000
x = 12000 - 4800
x = 7200
Hence,
The amount to be invested at 10% = 7200
The amount to be invested at 15% = 4800
**********************************************************
Exercise - 4.3
*) Solve each of the following pairs of equations by reducing them to a pair of linear equations.
Example 1): Solve the following pair of equations
2 + 3 = 13 and 5 - 4 = -2
x y x y
sol) Observe the given pair of equations.They are not linear equations(why?)
we have
2(1/x) + 3(1/y) = 13 ----(1)
5(1/x) - 4(1/y) = -2 ----(2)
if we substitute (1/x)=p & (1/y)=q, we get the following pair of linear equations:
2p + 3q = 13 ----(3)
5p - 4q = -2 -----(4)
Coefficients of "q" are "3" and "4" and their l.c.m is 12. Using the elimination method:
eq(3) * 4 8p +
eq(4) * 3 15p -
23P = 46
"q" terms have opposite sign,so we add the two equations
p = 46/23 = 2
substitute the value of"p" in eq(3)
2(2) + 3q = 13
3q = 13 - 4
3q = 9
q = (9/3) = 3
but (1/x) = p = 2 ---------->x = (1/2)
(1/y) = q = 3 --------------> y = (1/3)
*************************************************
Example 2). Kavitha thought of constructing 2 more rooms in her house. She enquired about the labour. She come to know that 6 men and 8 women could finish this work in 14 days. When she enquired , she was told that 8 men and 12 women could finish the work in 10 days. Find out that how much time would be taken to finish the work if one man or one woman worked alone?
sol) Let the time taken by one man to finish the work = x days
work done by one man in one day = (1/x)
Let the time taken by one women to finish the work = y days
work done by one woman in one day = (1/y)
Now, 8 men and 12 women can finish the work in 10 days.
So work done by 8 men and 12 women in one day = (1/10)---(1)
Also, work done by 8 men in one day is 8*(1/x) = 8/x
Similarly, work done by 12 women in one day is
12*(1/y) = (12/y)
Total work done by 8 men and 12 women in one day =
8 + 12 = 1 --------(2)
x y 10
equating (1) and (2)
8 + 12 = 1
x y 10
10( 8 + 12 ) = 1
x y
80 + 120 = 1 ------(3)
x y
Also, 6 men and 8 women can finish the work in 14 days.
Work done by 6 men and 8 women in one day:-
6 + 8 = 1
x y 14
14( 6 + 8) =1
x y
84 + 112 = 1 -----(4)
x y
Observe equations (3) and (4) are they linear equations? How do we solve then?We can
convert them into linear equations by substituting (1/x) =u and (1/y)=v
Equation(3) becomes=>80u +120v = 1--(5)
Equation(4) become=>84u + 112v = 1--(6)
L.C.M of 80 and 84 is 1680. using elimination method.
eq(3) *21
=> 21(80u+120v) =1
=> 1680u +2520v = 21 ---(7)
eq(4) * 20
=> 20(84u +112v) = 1
=> 1680u +2240v = 20---(8)
subtract (7)&(8) we get,
1680u +2520v = 21
1680u +2240v = 20
(-) (-) (-)
280v = 1
v = (1/28)
substitute"v" in eq(5) we get,
80u + 120*(1/280) = 1
80u = 1 - (3/7)
80u = (4/7)
u = 4 * 1
7
so one man can finish in (u)=140 days
one woman alone can in (v)= 280 days
**************************************************
Example 3). A man travels 370 km partly by train and partly by car. If he covers 250km by train and the rest by car, it takes 4hours. But if he travels 130 km by train and the rest by car, it takes 18 minutes more. find the speed of the train and that of the car.
sol) Let the speed of the train = x km/hr
Let the speed of the car = y km/hr
****************
we know that
Time = Distance
speed
****************
Situation 1:-Time spent travelling by train
=> 250 hrs
x
2). time spent travelling by car
=> 120 hrs
y
*) total time taken= Time spent in train + time spend in car
=> 250 + 120
x y
But, total time of journey is 4hours, so
250 + 120 = 4
x y
125 + 60 = 2
x y ----------(1)
Again ,When he travels 130 km by train and the rest by car
Time taken by him to travel 130 km by train
= 130 hrs
x
Time taken by him to travel 240 km(370-130) by car
= 240 hrs
y
Total time taken:-
130 + 240
x y
But given, time of journey is 4hrs 18min
i.e, 4*(
=> 4*(3 )hrs
10
or
=> (40+3)
10
=> 43
10
So, 130 + 240 = 43---> (2)
x y 10
substitute( 1/x)=a and( 1/y)=b in eq(1)&(2)
we get,
125a +60b = 2 -----(3)
130a +240b = 43 ------(4)
10
for 60 and 240. L.c.m is 240. using the elimination method.
eq(3)*4 => 500a +240b =8
eq(4)*1 => 130a +240b =43
(-) (-) 10
370a = 8 - 43
10
=> 370a = 80 - 43
10
=> 370a = 37
10
a =
10
a = 1
100
substitute a = 1 in eq(3)
100
5 + 60b = 2
4
5 -2 = -60b
4
5 - 8 = -60b
4
-3 = -60b
4
3 * 1 = b
4 60
1 = b
80
so, a = 1
100
and b = 1
80
so 1 = 1
x 100
1 = 1
y 80
x = 100 km/hr
y = 80 km/hr
so, speed of train was 100 km/hr and speed of car was 80 km/hr
******************************************************
Exercise - 4.3
1) 5 + 1 = 2
x - 1 y -2
6 - 3 = 1
x - 1 y -2
sol) 5 ( 1 ) +1 ( 1 ) = 2 ------ (1)
x - 1 y -2
6 ( 1 ) - 3 ( 1 ) = 1 -------- (2)
x - 1 y - 2
if we substitute 1 = p and 1 = q
x - 1 y -2
we get ,
5p + 1q = 2 ----- (3)
6p -3q = 1 ------ (4)
Using elimination method
multiply eq. (3) with 3 and adding to eq, (4), we get
3 * ( 5p + q = 2 )
15p +3q = 6
now,
15p + 3q = 6
6p - 3q = 1
21p = 7
=> p = 7 / 21 = 1 / 3
substitute the value of "p" in eq (3)
=> 5p + q = 2
=> 5( 1 / 3) + q = 2
=> 5 / 3 + q = 2
=> q = 2 - 5 / 3
=> q = 6 - 5
3
=> q = 1 / 3
But , 1 = p
x - 1
=> 1 = 1
x - 1 3
=> 3 = x - 1
=> 3 +1 = x
=> x = 4
Also, 1 = q
y- 2
=> 1 = 1
y - 2 3
=> 3 = y -2
=> 3 + 2 = y
=> y = 5
.^. x = 4 and y = 5
****************************************************************
2) x + y = 2
xy
x - y = 6
xy
sol)
1 + 1 = 2 -------- (1)
y x
y x
substitute 1 / y = p and 1 / x = q in (1) and (2)
we get
p + q = 2 ---- (3)
p - q = 6 ------ (4)
Subtract (3) (4)
p + q = 2
p - q = 6
2p 8 => p = 8 / 2 = 4
substitute "p" value in eq. (3)
p + q = 2
4 + q = 2
q = 2 - 4
q = -2
But , 1 / x = p
=> 1 / x = 4
= > x = 1 / 4
Also , 1 / y = q
=> 1 / y = -2
=> y = -1 / 2
.^. x = 1 /4 and y = -1 / 2
**********************************************************
3)
Sol)
Equation (1) and (2) will become
2p + 3q = 2 -------------(3)
4p - 9q = -1 ---------- (4)
Using elimination method
multiply eq (3) by 2 , we get,
2 ( 2p + 3q = 2) => 4p + 6q = 4
4p +6q = 4
4p - 9q = -1
- + +
0 15q = 5
15q = 5
q = 5 / 15 = 1 / 3
substitute value of "q" in eq (3)
2p + 3q = 2
2p + 3( 1 / 3) = 2
2p + 1 = 2
2p = 2 - 1
2p = 1
p = 1 / 2
squaring on both sides we get
=> 1 / x = 1 / 4
=> x = 4
Also
=> 1/ y = 1 / 9
=> y = 9
.^. x = 4 and y = 9
************************************************************
4) 6x + 3y = 6xy
2x + 4y = 5xy
sol) 6x + 3y = 6
xy
6
6 + 3 = 6 -------- (1)
y x
2x + 4y = 5
xy
2x + 4y = 5
xy xy
2 + 4 = 5 ----------- (2)
y x
Replace 1 / x = p and 1 / y = q
eq (1) and (2) becomes,
=> 6q + 3p = 6 ------ (3)
=> 2q + 4p = 5 ------- (4)
Using elimination method
multiply (4) by 3 , it becomes
3 * ( 2q + 4p =5 ) => 6q + 12p = 15
Now subtract
6q + 3p = 6
6q + 12p = 15
- - -
-9p = -9
-9p = 9
p = 1
Substitute "p" in (3) we get "q" value
=> 6q + 3p = 6
=> 6q + 3 (1) = 6
=> 6q = 6-3
=> 6q = 3
=> q = 3 / 6
=> q = 1 / 2
But , 1 / x = p
1/x = 1
x = 1
And , 1 / y = q
= 1 /2
1 / y = 1/2
y = 2
.^. x = 1 and y = 2
**********************************************************
5) 5 - 2 = -1
x + y x - y
15 + 7 = 10
x + y x - y
sol) 5 ( 1 ) - 2 ( 1 ) = -1
x + y x - y
15 ( 1 ) + 7 ( 1 ) = 10
x + y x -y
--------------------------------------------
Replace 1 = p and 1 =q
x + y x - y
---------------------------------------------
We get the following pair of linear equations
5 p - 2q = -1 ------ (3)
15p - 7q = 10 --------(4)
Using elminination method
Multiply eq (3) by 3 , we get
3* ( 5p -2q = -1 ) => 15p - 6q = -3
now,
15p - 6q = -3
15p + 7q = 10
- - -
-13q = -13
-
Substitute 'q" in eq. (3) we get
5p - 2 q = -1
5p - 2(1) = -1
5p - 2 = -1
5p = -1 +2
5p = 1
p = 1 / 5
But , 1 = p
x + y
1 = 1
x + y 5
=> 5 = x + y
=> 5 -x = y --------------- (4)
Also, 1 = q
x - y
1 = 1
x - y
=> x - y = 1 ------ (5)
substitute eq (4) , y = 5-x in eq. (5) we get
=> x - y = 1
=> x - (5 - x) = 1
=> x - 5 +x = 1
=> 2x -5 = 1
=> 2x = 1 + 5
=> 2x = 6
=> x = 6 / 2
=> x = 3
substitute x = 3 in eq. (4) we get
=> y = 5 - x
=> y = 5 - 3
=> y = 2
.^. x = 3 and y = 2
***************************************************************
6) 2 + 3 = 13
x y
5 - 4 = -2
x y
sol) 2 ( 1 ) + 3 ( 1 ) = 13------ (1)
x y
5 ( 1 ) -4 ( 1 ) = -2 ----- (2)
x y
--------------------------------------
Let 1 = p and 1 = q
x y
--------------------------------------
We get the following pair of linear equations.
2p + 3q = 13 ----------- (3)
5p - 4q = -2 -------------(4)
Using elimination method :-
multiply eq.(3) by 4
multiply eq.(4) by 3
we get,
4 *( 2p + 3q = 13) => 8p + 12q = 52
3* ( 5p - 4q = -2) => 15p - 12q = -6
23p = 46
=> p =
substitute p = 2 in eq.(1)
we get,
2p + 3q = 13
2(2) + 3q = 13
4 + 3q = 13
3q = 13 - 4
3q = 9
q = 3
But, 1 = p
x
1 = 2
x
=> x = 1
2
Also, 1 = q
y
1 = 3
y
=> y = 1
3
.^. x = 1 and y = 1
2 3
*************************************************************
(7) 10 + 2 = 4
x + y x - y
15 - 5 = -2
x + y x - y
sol) 10 ( 1 ) + 2 ( 1 ) = 4
x + y x - y
15 ( 1 ) - 5 ( 1 ) = -2
x + y x - y
--------------------------------------------------
let 1 = p and 1 = q
x + y x - y
----------------------------------------------------
We get the following pair of linear equations
10p + 2q = 4 ------ ( 3)
15p - 5q = -2 --- ---(4 )
Using elimination method :-
Multiply (eq.3) *5 and (eq.4) * 2
we get,
5 * (10p + 2q =4) => 50p +10q= 20
2*(15p - 5q = -2) => 30p -10q = -4
80p = 16
=> p = 16
80
substitute "p" value in (eq.3)
=> 10p + 2q = 4
=> 10(
=>
=>2 + 2q = 4
=> 2q = 4 - 2
=> 2q = 2
=> q = 1
But , 1 = p
x + y
1 = 1
x + y 5
=> 5 = x + y ------ ( 5)
Also, 1 = q
x - y
1 = 1
x - y
=> x - y = 1
=> y = x - 1 ------- (6)
substitute (eq.6) in (eq.5)
we get,
5 = x + y
5 = x + x - 1
5 = 2x -1
5 +1 = 2x
6 = 2x
3 = x
put x = 3 in (eq.6)
y = x - 1
y = 3 - 1
y = 2
.^. x = 3 and y = 2
******************************************************************
8) 1 + 1 = 3
3x + y 3x - y 4
1 - 1 = -1
2(3x +y) 2(3x - y) 8
sol) Let 1 = p and 1 = q
3x + y 3x - y
We get the following pair :-
p + q = 3 ---------------(1)
4
1 p - 1 q = -1 ------(2)
2 2 8
Using elimination method :-
Multiply (eq.1) * (1/2) and adding to (eq.2). we get,
1 p + 1 q = 3
2 2 8
1 p - 1 q = -1
2 2 8
1 +1 p = 3 - 1
2 8
=>
=> p = 1
4
substitute "p" in (1) we get,
=> p + q = 3
4
=> 1 + q = 3
2 4
=> q = 3 - 1
4 2
=> q = 2
4
=> q = 1
2
But , 1 = p
3x+y
1 = 1
3x + y 4
=> 4 = 3x + y
=> y = 4 - 3x ---------- (3)
Also, 1 = q
3x - y
1 = 1
3x - y 2
=> 2 = 3x - y -------(4)
substitute the value of (eq. 3) in (eq.4)
=> 2 = 3x - y
=> 2 = 3x -( 4 - 3x)
=> 2 = 3x - 4 +3x
=> 2 = 6x - 4
=> 2 + 4 = 6x
=> 6 = 6x
=> x = 1
put x = 1 in (eq.3)
y = 4 - 3x
y = 4 - 3(1)
y = 4 -3
y = 1
.^. we got x = 1 and y = 1.
**************************************************************
2) Formulate the following problems as a pair of equations and then find their solutions.
1) A boat goes 30km upstream and 44km downstream in 10hrs. In 13 hrs it can go 40km upstream and 55km downstream. Determine the speed of the stream and that of the boat in still water.
sol) Let speed of the boat in still water = x km/hr
Let speed of the stream = y km/hr
Speed downstream = Speed of boat in still water + Speed of stream
= x + y
Speed upstream = speed of boat in still water - speed of stream
= x - y
-------------------------------------------------
We have formula => Time = Distance
Speed
-------------------------------------------------
Time taken to cover 30km upstream
= 30hrs.
x - y
Time taken to cover 44km downstream
= 44 hrs
x + y
But Total time of journey is 10hrs.
30 + 44 = 10 -----------(1)
x - y x + y
2nd condition :-
Time taken to cover 40km upstream
= 40 hrs
x - y
Time take to cover 55km downstream
= 55 hrs
x + y
But, total time journey is 13hrs
40 + 55 = 13 ---- (2)
x - y x + y
------------------------------------------------------
substitute 1 = p and 1 = b
x - y x + y
-----------------------------------------------------
we get
30p + 44q = 10 ----- (3)
40p + 55q = 13 ------ (4)
Using elimination method
Multiply (eq.3) * 4 and (eq.4) *3 and subtracting
120p + 176q = 40
120p + 165q = 39
- - -
11q = 1
q = 1
11
Subs "q" value in (eq.3)
we get,
30p +
30p + 4 = 10
30p = 10 - 4
30p = 6
p = 6
30
p = 1
5
But , 1 = p
x - y
1 = 1
x - y 5
=> 5 = x - y ---------- (5)
Also, , 1 = q
x + y
1 = 1
x + y 11
=> 11 = x + y ----------- (6)
solving (eq.5) and (eq.6) we get,
x - y = 5
x + y = 11
2x = 16
x =
2
put x = 8 in (eq.5)
x - y = 5
8 - y = 5
8 - 5 = y
y = 3
Hence , speed of boat in still water = 8km/hr
Speed of stream = 3 km/hr
***********************************************************
2). Rahim travels 600km to his home partly by train and partly by car. He takes 8 hours if he travels 120 km by train and rest by car. He takes 20 minutes more if he travels 200km by train and rest by car. Find the speed of the train and the car.
sol) Let speed of the train be = x km/hr
Let speed of the car be = y km/hr
Formula :- Time = Distance
Speed
condition 1) :- he takes 8hrs if he travels 120km by train and rest by car.
Time spent travelling by train = 120
x
------------------------------------------------
total km = 600
600( total) - 120(train ) = 480 (car)
------------------------------------------------
Time spent travelling by car = 480
y
In total 8 hrs = Time spent in train + Time spent in car
8 = 120 + 480 ----------- (1)
x y
condition 2 :- Take 20min more ( i.e, 8hr 20 min) if travel 200km by train.
Time taken to travel 200km by train = 200
x
Time taken to travel rest km by car = 400
y
total time( 8hr, 20min ) = 200 + 400 --(2)
x y
======================
8hr 20min = 8 *
= 8 * 1 hrs
3
= 25
3
======================
Substitute (1/x) = p and (1/y) = q in eq.(1) and eq. (2)
we get,
120p + 480q = 8 ----- (3)
200p + 400q = 25 ----- (4)
3
3 3
p + 4q = 1
15 -------------- (5)
p + 2q = 1
24 ---------------(6)
2q = 1 - 1
15 24
2q = 24 - 15
360
2q = 9
360
2q = 1
40
q = 1
2*40
q = 1
80
substitute "q" in (eq.5) we get,
p +
p + 1 = 1
20 15
p = 1 - 1
15 20
p = 20 -15
300
p = 5
300
p = 1
60
But , 1 = p
x
1 = 1
x 60
=> x = 60
Also, 1 = q
y
1 = 1
y 80
=> y = 80
So, Speed of train = 60 km/hr
Speed of car = 80 km/hr
********************************************************
3) 2 women and 5 men can together finish an embroidery work in 4 days, while 3 women and 6 men can finish it in 3 days. Find the time taken by 1 woman alone to finish the work, and also that taken by 1 man alone to finish the work.
sol) Let time taken by 1 woman to finish the work = x days
Work finished by 1 woman in 1 day = 1
x
Let time taken by 1 man to finish the work = y days
Work finished by 1 man in 1 day = 1
y
Condition 1 :-
2 women and 5 men complete the work in 4 days
.^. Work finished by 1 woman and 5 men in 1 day = 1/4
2 * ( Work finished by 1 woman in 1 day ) +
5* ( Work finished by 1 man in 1 day ) = 1
4
2 * 1 + 5 * 1 = 1
x y 4
2 + 5 = 1
x y 4 ---------------- (1)
Condition 2 :-
3 women and 6 men complete the work in 3 days
.^. Work finished by 3 women and 6 men in 1 day = (1/3)
3 *( Work finished by 1 woman in 1 day ) +
6* ( Work finished by 1 man in 1 day ) = 1
3
3 * 1 + 6 * 1 = 1
x y 3
3 + 6 = 1
x y 3 ---------- (2)
Let 1 = p and 1 = q
x y
eq.(1) and eq.(2) becomes,
2p + 5q = 1
4
=> 4( 2p + 5q ) = 1
=> 8p + 20q =1 ----(3)
3p + 6q = 1
3
=> 3(3p + 6q ) = 1
=> 9p + 18q = 1 -----(4)
Using elimination method.
Multiply (eq.3) *9 and (eq.4) * 8 and subtracting
9* ( 8p + 20q = 1)
8* (9p + 18q =1)
= > 72p +180q = 9
=> 72p + 144q = 8
- - -
36q = 1
=> q = 1
36
Substitute value of "q" in (eq.3)
8p + 20q = 1
8p + 20 ( 1 ) = 1
36
8p + 5 ( 1 ) = 1
9
72p + 5 = 9
72p = 9 -5
p = 4
72
p = 1
18
But, 1 = p
x
1 = 1
x 36
=> x = 36
Also, 1 = q
y
1 = 1
y 18
=> y = 18
Thus, One woman alone can finish work in 36 days. One man alone can finish work in 18 days
**************************************************
(*)Optional exercise:-
1) Animals in an experiment are to be kept on a strict diet. Each animal is to receive among other things 20g of protein and 6g of fat.
The laboratory technicians purchased two food mixes, A and B. Mix A has 10% protein and 6% fat. Mix B has 20% protein and 2% fat. How many grams of each mix should be used?
sol) Let "A" and "B" be the required grams of mixes of A and B respectively
Each animal getting protein :- 10%A + 20%B
10 A + 20 B
100 100
(0.1)A + (0.2)B
0.1A + 0.2B
Given:- each animals should get 20g of protein
.^. 0.1A + 0.2B = 20------(1)
Each animals should get fat = 6g
6%A + 2%B = 6
6 A + 2 B = 6
100 100
(0.06)A + (0.02)B = 6 ------(2)
now
Multiply eq(1) with 10 and eq(2) with 100
we get,
{(0.1)A +(0.2)B = 20 } * 10
{(0.06)A +(0.02)B = 6 } * 100
A + 2B = 200 -----(3)
6A + 2B = 600------(4)
subtract eq(3) and eq(4)
A + 2B = 200
6A + 2B = 600
(-) (-) (-)
-5A -0 =-400
5A = 400
A = 400/5
A = 80
substitute A=80 in (3) we get
80 + 2B = 200
2B = 200-80
2B = 120
B = 120/2
B = 60
.^. Mix A should be 80g and Mix B should b 60g to b used to get 20g of protein and 6g of fat for each animals.
*************************************************






















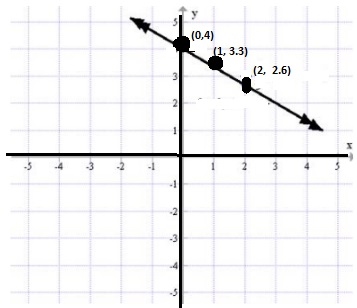








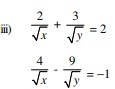


wow first see 4.2 exercise u wrote 7×2000=140000 who will learn maths in this web site they fail 100%
ReplyDeleteThank you for pointing out the mistake. If you find anymore mistakes do mention it..keep visiting the site
Delete1st problem
ReplyDeleteI love this site im doing my homework using your site thaxs sir
ReplyDeleteYou welcome.
DeleteBROTHER I LOVED YOUR SITE I AM DOING GOOD NOW TQ BROTHER I WANT TO DO PAYTM BUT THERE IS NO MONEY IN MY ACCOUNT SORRY BRO
ReplyDeleteNo problem Brother,Hope you find it helpful.If u need anything more please do mention it.I will b happy to help u
Deleteplease provide the answers short
ReplyDeleteits too long