(*) let us observe two situation
1). A flower bed in a garden is in the shape of a triangle. The longest side is 3 time the middle side and smallest side 2 units shorter than the middle side. Let P represent the length of the middle side, then what's the perimeter in terms of P?
2) The length of a rectangular dining hall is twice its breadth . Let x represent the breadth of the hall. What is the area of the floor of the hall in terms of x?
In the above situations, there is an unknown in each statement. In the first situation, middle side is given as 'P' units.
Since,
Perimeter of triangle = sum of all sides
perimeter = P + 3P + P - 2
= 5P - 2
Similarly in the second situations, length is given as twice the breadth.
So, if breadth = x, length = 2x
Since area of rectangle = L * b
Area = (2x)(x)
= 2x^2
As you know, the perimeter,
5P-2 of the triangle and area 2x^2 of the rectangle are in the form of polynomials of different degrees.
(*) What are Polynomials :
Polynomials are algebraic expressions constructed using constants and variable.
Coefficients operate on variables, which can be raised to various powers of non-negative integer exponents.
For example,
2x+5
3x^2 + 5x + 6
-5y,
x^3 are some polynomials.
1 , 1 , 1 , √3x^3 etc.
x^2 √2x y - 1
are not polynomials.
why is 1 not a polynomial? Discuss with
y - 1
your friends and teacher.
*****************************************
(*) Degree of a polynomial
Recall that if p(x) is a polynomial in x, the highest power of x in p(x) is called the degree of the polynomial p(x).
For example, 3x + 5 is a polynomial in the variable x . It is degree 1 and is called a linear polynomial.
5x, √2y + 5 , 1/3 p, m+1 etc, are some more linear polynomials.
A polynomial of degree 2 is called a quadratic polynomial.
For example, x^2 + 5x + 4 is a quadratic polynomial in the variable x.
2x^2 + 3x - (1/2)
p^2 - 1 ,
3-z-z^2
y^2 - (y/3) + √2 are examples of quadratic polynomials.
The expression 5x^3 - 4x^2 + x - 1 is a polynomial in the variable x of degree 3, and is called a cubic polynomial.
Some more examples of cubic polynomials are
2- x^3
p^3
L^3 - L^2 - L + 5.
We can write polynomials of any degree.
7u^6 -(3/2)u^4 + 4u^2 - 8 is polynomial of degree 6 and x^10 - 3x^8 + 4x^5 + 2x^2 - 1 is a polynomial of degree 10
*****************************************
We can write a polynomial in a variable x of a degree n where n is any natural number.
Generally, we say
p(x) = a0 x^n + a1 x^n-1 + a2 x^n-2....+a n-1 + an is a polynomial of nth degree.
Where a0, a1, a2....an-1, an are real coefficients and a0 =/= 0.
For example, the general form of a first degree polynomial in one variable x is ax+b, where a and b are real numbers and a =/= 0.
*****************************************
(*) Value of a polynomial
Now consider the polynomial p(x) = x^2 -2x - 3.
What is the value of the polynomial at any point?
example, what is the value at x = 1?
put x = 1 , in the polynomial, we get
p(1) = (1)^2 - 2(1) - 3 = -4.
The value -4, is obtained by replacing x by 1 in the given polynomial p(x). This is the value of
x^2 - 2x - 3 at x = 1.
Similarly, p(0) = -3 is the value of p(x) at x = 0
Thus, if p(x) is a polynomial in x , and if k is a real number, then the value obtained by replacing x by k in p(x), is called the value of p(x) at x = k, and is denoted by p(k).
*****************************************
(*) Zeroes of a Polynomial:
What are values of
p(x) = x^2 - 2x - 3 at x = 3, -1 and 2?
We have,
p(3) = (3)^2 - 2(3) - 3= 9 - 6 - 3 = 0
p(-1) = (-1)^2 -2(-1)-3 = 1 +2 - 3 = 0
p(2) = (2)^2 - 2(2) - 3 = 4-4-3= -3
We see that
p(3) = 0
P(-1) = 0.
these points, x = 3 and x = -1, are called zeroes of the polynomial
p(x) = x^2 - 2x - 3.
As p(2) =/= 0,
2 is not the zero of p(x).
More generally , a real number k is said to be a zero of a polynomial
p(x), if p(k) = 0
*****************************************
Exercise - 3.1
What is the coefficient :- A number (1.2.3.4.....) used to multiply a variable ( x,y,z,a,b.....)
Example:- 7x, it means 7 times x, and "x " is a variable, so 7 is a coefficient.
*) Variables with no number have a co-efficient of "1"
Ex:- for "x" we can write as "1x"
Degree of a Polynomial :- The highest power of "x" in p (x) is called the degree of the polynomial
Ex :- p(x)= 3x +5 is a polynomial in the variable "x". it is of degree "1" and is called a linear polynomial.
Zero of a polynomial :- A real number "k" is a said to be a zero of a polynomial p(x), if
p ( k) = 0
----------------------------------------------------------------------------------
1) (a) If p (x) = 5x^7 - 6x^5 + 7x -6, find
(1) coefficient of x^5
sol) -6x^5 = -6
(2) degree of p (x)
sol) Highest degree of "x ", 5x^7 = 7
(3) constant term = -6
-------------------------------------------------------------------------------
(b) Write three more polynomials and create three questions for each of them.
1) if p(x) = 2x^2 + 5x - 6 , find coefficient of X^2?
2) if p (x) = 5x + 8 , find degree of p (x)
3) if p (x) = x^2 +3x- 4 what is the value of polynomial at point P ( 2 )?
***************************************************************
2) State which of the following statements are true and which are false? give reasons for your choice.
(1) The degree of polynomial _/2 x^2 - 3 x + 1 is _/2
Sol) False.
because _/2 is a co-efficient of x^2 not a degree . The degree of above equation is"2"
----------------------------------------------------------------------------------------------
(2) The coefficient of x^2 in the polynomial p (x) = 3x^3 - 4x^2+5x+7 is 2
sol) False.
Co-efficient of x^2 is -4x^2 = -4
-------------------------------------------------------------------------------------
(3) The degree of a constant term is zero.
Sol) True. For any constant term its degree is always zero
--------------------------------------------------------------------------
(4) 1 is a quadratic polynomial.
x^2 - 5x +6
sol) False, because polynomial should be in linear form ( p (x) )not in fractional ( 1/p(x) ) .
-------------------------------------------------------------------------------------------
(5) The degree of a polynomial is one more than the numbers of terms in it
sol) False . because degree of any polynomials never related with no.of terms
***********************************************************
3). If p ( t) = t^3 - 1 , find the values of
(1) p ( 1)
Sol) p (1) = (1) ^3 - 1 = 1-1 = 0
(2) p ( -1 )
Sol) p ( -1 ) = (-1)^3 - 1 = -1-1 = -2
(3) p ( 0 )
Sol) p ( 0 ) =( 0 ) ^3 - 1 = -1
(4) p ( 2)
Sol) p ( 2 ) = ( 2 ) ^ 3 - 1 = (2*2*2) - 1 = 8 -1 =7
(5) p ( -2)
sol) P ( -2) = ( -2 ) ^ 3 - 1 = ( -2 * -2 * -2 ) - 1 = -8 -1 - = -9
******************************************************
4. Check whether -2 and 2 are the zeros of the polynomial x^4 - 16
Sol ) Given , p (x ) = x ^4 - 16
=> p ( -2)
=> ( -2 ) ^ 4 - 16
=> (-2 * -2 * -2 * -2) - 16
=> 16 - 16 =0
2) p (2)
Sol) (2)^4 - 16
=> ( 2*2*2*2) - 16
=> 16-16
=> 0
Thus, "-2" and "2" are the zeros of the polynomial x^4 - 16.
**********************************************************
5. Check whether "3" and "-2" are the zeros of the polynomial p (x) when p (x) x^2 -x-6.
Sol ) p(x) = x^2 - x - 6
p(3) = (3) ^2 - (3) - 6
=> (3*3) -3-6
=> 9-9
= 0
2) p ( -2 )
Sol) ( -2 )^2 - (-2) -6
= ( -2 *-2 ) - (-2) -6
= 4 +2-6
= 0
Thus , Both 3 and -2 are the zeros of the polynomial x^2 - x - 6
******************************************************
(*) Working with polynomials
If k is a zero of p(x) = ax+b, a =/= 0
then p(k)= ak + b = 0.
i.e., k = (-b/a), or the zero of the linear polynomial
ax+b is (-b/a)
Thus, the zero of a linear polynomial is related to its coefficients, including the constant term.
(*) Graphical Representation of a Linear polynomial
Consider first a linear polynomial ax+b, a=/=0. we know that the graph of y= ax+b is a straight line.
Example : the graph of y = 2x + 3 is a straight line intersecting the y-axis at (0,3) and passing through the points (-2, -1) and (2,7)
from the graph we can see that the graph of y=2x+3 intersects the x-axis between x=-1 and
x = -2,
that is, at the point ( -3/2, 0).
or (-1.5 , 0)
-3/2 = -1.5
But x = -3/2 is also the zero of the polynomial 2x + 3.
Thus, the zero of the polynomial 2x+3 is the x-coordinate of the point where the graph of
y = 2x + 3 intersects the x - axis.
In general , for a linear polynomial ax+b, a=/=0, the graph of y = ax + b is a straight line which intersects the x-axis at exactly one point, namely,
(-b/a , 0 )
Therefore, the linear polynomial ax + b, a=/=0, has exactly one zero, namely, the x -coordinate of the point where the graph of y = ax + b intersects the x - axis.
*****************************************
(*) Graphical Representation of a Quadratic Polynomial
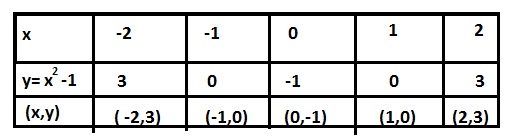
Consider the quadratic polynomial x^2 -3x - 4.
Let us see how the graph of y = x^2 - 3x - 4 looks like.
Let us list a few values of y = x^2 - 3x -4 corresponding to a few values of x
We locate the points listed above on a graph paper and draw the graph
Is the graph of this quadratic polynomial a straight line? it is like a V shape curve.
It intersects the x-axis at two points.
In fact, for any quadratic polynomial
ax^2 + bx = c, a=/=0, the graph of the corresponding equation y = ax^2 + bx + c either opens upwards V or open downwards like /\.
This depends on whether a>0 or a<0.
( The shape of these curves are called parabolas.)
We observe that -1 and 4 are zeroes of the quadratic polynomial and -1 and 4 are intersection points of x-axis.
Zeroes of the quadratic polynomial x^2 -3x-4 are the x-coordinates of the points where the graph of y=x^2 - 3x - 4 intersects the x-axis.
This is true for any quadratic polynomial, i.e., the zeroes of a quadratic polynomial
ax^2 + bx + c, are precisely the x - coordinates of the points where the parabola representing y= ax^3 + bx + c intersects the x-axis.
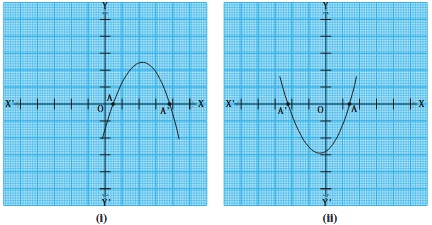
From our observation earlier about the shape of the graph of y = ax^2 + bx + c, the following three cases can happen:
Case(!) : Here, the graph cuts x-axis at two distinct points A and A'.
In this case, the x-coordinates of A and A' are the two zeroes of the quadratic polynomial ax^2 +bx + c. The parabola can open either upward or downward.
case(!!) : Here, the graph touches x-axis at exactly one point, i.e., at two coincident points.
So, the two points A and A' of Case(!) coincide here to become one point A.
The x-coordinates of A is the only zero for the quadratic polynomial ax^2 + bx + c
case(!!!) : Here, the graph is either completely above the x-axis or completely below the x-axis. So, it does not cut the x-axis at any point.
So, the quadratic polynomial ax^2 + bx + c has no zero in this case.
So, you can see geometrically that a quadratic polynomial can have either two distinct zeroes or two equal zeroes (i.e., one zero), or no zero.
This also means that a polynomial of degree 2 has atmost two zeroes.
(*) Geometrical meaning of zeroes of a Cubic Polynomial.
Consider the cubic polynomial x^3 - 4x.
To see how the graph of y= x^3 - 4x looks like, let us list a few values of y corresponding to a few values for x
On drawing the graph, we see that the graph of y = x^3 - 4x looks like
We see from the table above that -2, 0 and 2 are zeroes of the cubic polynomial x^3 - 4x.
-2, 0 and 2 are the x-coordinates of the points where the graph of y = x^3 - 4x intersects the x-axis. So this polynomial has three zeroes.
Let us take a few more examples.
Consider the cubic polynomials x^3
and x^3 - x^2 respectively
In y = x^3, you can see that 0 is the x-coordinate of the only point where the graph of y = x^3 intersects the x-axis.
So, the polynomial has only one distinct zero. Similarly, 0 and 1 are the co-ordinates of the only points where the graph of y= x^3 - x^2 intersects the x-axis. So, the cubic polynomial has two distinct zeroes.
From the examples above, we see that there are at most 3 zeroes for any cubic polynomial.
In other words, any polynomial of degree 2 can have at most three zeroes.
Remark : In general, given a polynomial p(x) of degree n, the graph of y = p(x) intersects the x-axis at most n points. Therefore, a polynomial p(x) of degree n has at most n zeroes.
Example -1. Look at the graphs in the figure given below.
Each is the graph of y = p(x), where p(x) is a polynomial. In each of the graphs, find the number of zeroes of p(x) in the given range of x.
sol) In the given range of x in respective graph :
(!) The number of zeroes is 1 as the graph intersects the x-axis at one point only.
(!!) The number of zeroes is 2 as the graph intersects the x-axis at two points.
(!!!) The number of zeroes is 3.
(!v) The number of zeroes is 1.
(V) The number of zeroes is 1.
(V!) The number of zeroes is 4.
*****************************************
Example-2. Find the number of zeroes of the given polynomials. And also find their values.
(!) p(x) = 2x + 1
sol) We will do this without plotting the graph.
To find zeroes,
Let p(x) = 0
So, 2x + 1 = 0
Therefore x = -1/2
The zero of the given polynomial is -1/2
*****************************************
(!!) q(y) = y^2 - 1
sol) It has atmost two zeroes.
To find zeroes,
let q(y) = 0
=> y^2 - 1 = 0
********************
y^2 - 1^2 = (a^2- b^2) form
*********************
=> (y+1)* (y-1) = 0
=> y = -1 or y = 1
Therefore the zeroes of the polynomial are -1 and 1
*****************************************
(!!!) r(z) = z^3
sol) It has at most three zeroes.
Let(z) = 0
=> z^3 = 0
=> z = 0
So, the zero of the polynomial is 0.
*****************************************
Exercise 3.2
1) The graphs of y= p (x) are given in the figure, for some polynomials p (x). In each case, find the number of zeros of p (x).
(1)
Sol ) The number of zeros is "0" as the graph does not intersect x-axis at any point.
*********************************************************************************
(2)
sol) The number of zeros is "1" as the graph intersects x-axis at one point only.
*********************************************************************************
(3)
sol) The number of zeros is "3" as the graph intersects x-axis at three points.
*********************************************************************************
(4)
sol) the number of zeros is "2" as the graph intersects x-axis at two points.
*********************************************************************************
(5)
sol) The number of zeros is "4" as the graph intersects x-axis at four points.
********************************************************************************
(6)
sol) The number of zeros is " 3" as the graph intersects x-axis at three points.
----------------------------------------------------------------------------------------------
2) Find the zeros of the given polynomials.
(1) p (x) = 3x
Sol) Since it is a linear polynomial. It has only one zero.
Let p(x) = 0
3x= 0
.^. x= 0
(2) p (x) = x^2 + 5x + 6
Sol ) Since its a quadratic polynomial. It has at most two zeros.
Let p (x) = 0
= > x^2 + 5x + 6 = 0
=> x^2 + 2x +3x +6= 0
=> (x^2 +2x) + (3x+6) = 0
=> (x *x + 2x) + (3x +2*3) = 0
Taking common, we get
= > x ( x + 2) + 3 (x + 2) = 0
As ( x + 2) is present in both sides ,take (x+2) as common we get
= > (x+2) (x + 3) = 0
=> x+2 = 0 x+3= 0
=> x= -2 or x=-3
.^. the zeros of the polynomial are -2 and -3
------------------------------------------------------------------------------------------------
3) p (x) = (x+2) (x+3)
sol) Let p (x) =0
=> (x+2) (x+3) = 0
=> x+2=0 or x+3=0
=> x= -2 or x= -3
.^. the zeroes of the polynomial are -2 and -3
------------------------------------------------------------------------------------------------
4) p (x) = x^4 - 16
sol) let p(x) = 0
=> x^4 - 16 = 0
we have (a)^2 - (b)^2 = (a+b) ( a-b) by using this formula we can write x^4-16 as
we can write for x^4 = ( x^2)^2 and 16= (4)^2
where a = x^2 , b = 4
=> (x^2)2 - (4) ^2 = (x^2 + 4) ( x^2 - 4) = 0
=> (x^2 +4) (x^2 - 4) = 0
=? x^2 +4 = 0 or x^2 - 4 = 0
=> x^2 = -4 or x^2 = 4
=> x = _/-4 or x = _/4
=> x = _/ (-2) ^2 or x = _/ (2)^2
x= -2 or x = 2
*******************************************************************
3 Draw the graph of the given polynomial and find the zeroes. justify the answers.
(1) p(x) = x^2 - x - 12
Sol ) p (x) = 0
=> x^2 - x - 12 = 0
=> x^2 - 4x +3x- 12 = 0
=>(x *x - 4*x) + (3*x - 3*4 )= 0
taking common we get
=> x (x - 4) + 3 (x-4) = 0
taking (x-4) as common
=> (x-4) (x+3) = 0
=> x-4 = 0 or x+3=0
x=4 and x=-3
We got zeros of this polynomial x^2-x-12 as 4, -3 lets prove it by graph
y= x^2 - x - 12 intersects x-axis at x= -3 and x=4 as shown in the above graph
hence, x=-3 and x=4 are zeros of polynomial.
-------------------------------------------------------------------------------------------------
2) p(x) = x^2 - 6x +9
Sol) x^2 -6x+9=0
=> x^2 -3x-3x+9=0
=> x(x-3) -3 (x-3)= 0
=> (x-3) (x-3) = 0
=> x=3
Lets draw the graph
Graph :-
y= x^2 -6x+9 intersects x-axis at x=3
Hence x=3 is a zero of for given polynomial.
--------------------------------------------------------------------------------------------------
(3) p (x) = x^2 -4x +5
sol) x^2 - 4x +5 = 0
=> x^2 - 5x +x +5 = 0
=> x(x-5)+ 1(x+5)=0
As we can see we not able to get any zeros for this polynomial.
Draw the graph
Graph :-
y= x^2-4x+5 does not intersect at x-axis
Hence, there are no zeros for given polynomial.
--------------------------------------------------------------------------------------------
(4) p(x) = x^2 +3x - 4
Sol) x^2 +3x-4=0
=> x^2 + 4x -x - 4 = 0
=> x(x +4) -1 (x+4) = 0
=> (x+4) (x-1) = 0
=> x=-4 or x=1
We got zeros of this polynomial x^2 +3x-4 as x=-4 and x=1
Draw the graph
GRAPH:-
y= x^2+3x-4 intersects x-axis at x=1, x=-4
Hence, x=1 and x=-4 are zeros of a given polynomial.
------------------------------------------------------------------------------------------------
(5) p(x) = x^2 - 1
sol) Let x^2 - 1 = 0
it is in the form of a^2 - b^2 = (a+b) (a-b)
we can write for x^2 - 1 as x^2 - 1^2
where a=x, b=1
=> x^2 - 1^2 = (x+1) (x-1)
=> (x+1) (x-1) = 0
=> x=-1 or x=1
We got zeros of this polynomial x^2-1 as x= -1 and x=1
Draw the graph
GRAPH :-
y= x^2 - 1 intersects x-axis at x= - 1 and x=1
Hence , x = -1 and x= 1 are zeros of a given polynomial.
------------------------------------------------------------------------------------------------
4. Why are 1/4 and -1 zeros of the polynomials p (x) = 4 x^2 +3x -1?
Sol) let p(x) = 4 x^2 +3x -1
let P ( 1/4)
= 4 (1/4)^2 + 3 (1/4) -1
= 4 * 1/16 + 3*1/4 - 1
= 1/4 + 3/4 -1
= 1+3 -1
4
= 4/4 - 1
= 1 -1
= 0
(2) p ( -1)
= 4 ( -1)^2 + 3 ( -1) -1
= 4 -3-1
= 4-4
=0
Hence , p ( 1/4) and p (-1) are zeros of the polynomial p (x) = 4x^2 +3x-1
***************************************************************
Example-3. Find the zeroes of the quadratic polynomial x^2 + 7x +10, and verify the relationship between the zeroes and the coefficients.
sol) We have
x^2 + 7x + 10 = x^2 + 2x + 5x +10
= x(x+2)+5(x+2)
= (x+2)(x+5)
So, the value of x^2=7x=10 is zero when x+2=0 or x+5=0
i.e., when x = -2 or x = -5
Therefore, the zeroes of
x^2 +7x+10 are -2 and -5
Now,
sum of the zeroes = -2+(-5) = -(7)
= -(7) = - (coefficient of x)
1 coefficient of x^2
product of the zeroes = -2 *(-5) = 10
= 10 = constant term
1 coefficient of x^2
****************************************
Example-4. Find the zeroes of the polynomial x^2-3 and verify the relationship between the zeroes and the coefficients.
sol) Recall the identity
a^2 - b^2 = (a-b)(a+b)
using it, we can write;
x^2-3 = (x -√3) (x + √3)
So, the value of x^2 - 3 is zero when
x = √3 or x = -√3
Therefore, the zeroes of x^2 - 3 are
√3 and -√3
Sum of the zeroes:
= √3 + (-√3) =0 = -(coefficient of x)
coefficient of x^2
(*) Product of zeroes :
=√3 * (-√3) = -3 = -3 = constant term
1 coefficient of x^2
*****************************************
Example-5. Find a quadratic polynomial, the sum and product of whose zeroes are -3 and 2, respectively.
sol) Let the quadratic polynomial be ax^2+bx+c, and its zeroes be 𝛼 and 𝛃 .
We have
𝛼 + 𝛃 = - 3 = -b
a
and 𝛼𝛃 = 2 = c
a
If we take a = 1 , then b = 3 and c = 2
So, one quadratic polynomial which fits the given conditions is x^2 + 3x + 2.
Similarly, we can take 'a' to be any real number.
Let us say it is k.
This gives -b/k=-3
or b = 3k and c/k = 2 .
Putting the values of a,b and c, we get the polynomial is
kx^2 + 3kx + 2k.
*****************************************
Example-6. Find a quadratic polynomial if the zeroes of it are 2 and -1/3 respectively.
sol) Let the quadratic polynomial be
ax^2 + bx +c, a =/= 0 and its zeroes be 𝜶 and 𝛃
Here 𝜶=2 , 𝛃 = -1/3
Sum of the zeroes = ( 𝜶 + 𝛃 ) = 2 + (-1/3) = 5/3
product of the zeroes = (𝜶𝛃 ) = 2(-1/3) = -2/3
Therefore the quadratic polynomial
ax^2 + bx + c is
k[x^2 - (𝜶 + 𝛃 )x + 𝜶𝛃 ],
where k is a constant
= k [x^2 - (5/3)x - (2/3)]
We can put different values of k.
When k = 3, the quadratic polynomial will be
3x^2 -5x - 2.
*****************************************
Example-7. verify that 3,-1, -1/3 are the zeroes of the cubic polynomial p(x) = 3x^3 - 5x^2 - 11x - 3, and then verify the relationship between the zeroes and the coefficients.
sol) Comparing the given polynomial with
ax^3 + bx^2 + cx +d, we get
a = 3,
b = -5,
c = -11,
d = -3. Further.
p(3) = 3 * 3^3 - (5*3^2) - (11*3) - 3
= 81 - 45 - 33 - 3 = 0.
p(-1) = 3 * (-1)^3 - 5*(-1)^2 - 11*(-1)-3
= -3-5+11-3=0
p(-1/3) = 3*(-1/3)^3 - 5*(-1/3)^2 - 11*(-1/3) - 3
= -1/9 - (5/9) +(11/3) - 3
= -2/3 + (2/3) = 0
Therefore, 3, -1, and -1/3 are the zeroes of
3x^3 - 5x^2 - 11x - 3.
So, we take 𝝰 = 3, 𝛃 = -1 and 𝜸=(-1/3)
Now,
𝝰 +𝛃 +𝜸 = 3 + (-1) + (-1/3)
= 2 - (1/3)
= (5/3) = -(-5) /3 = - b/a
𝝰𝛃 + 𝛃 𝜸 +𝜸𝝰 = 3*(-1) + (-1) * (-1/3) + (-1/3 * 3
= -3 + (1/3) - 1
= -(11/3) = c/a
𝝰𝛃 𝜸 = 3* (-1)*(-1/3) = 1
= -(-3) / 3 = -d/a.
******************************************
Exercise - 3.3
1) Find the zeros of the following quadratic polynomials and verify the relationship between the zeros and the coefficients.
(1) x^2 - 2x - 8
sol) there are two parts in the question 1) finding zeros and 2) verifying
(1) Finding zeros of the quadratic polynomial ( x^2 -2x -8)
p(x) = x^2 -2x -8
Let p(x) = 0
x^2 - 2x - 8 = 0
splitting the middle term "-2x"
x^2-4x+2x-8 = 0
x(x -4) +2( x-4) = 0
(x-4) (x+2) = 0
x=4 and x=-2
2nd) Verifying the relationship between zeros ( -2 , 4 )of the polynomial and the coefficients
p(x) = x^2 - 2x - 8 = 1 x^2 - 2x - 8
comparing with quadratic form ax^2 +bx +c
we get
a= 1
b= -2
c= -8
Verification :-
1) sum of zeros = -- Coefficient of x
Coefficient of x^2
that is , alpha + beta = -- b
a
*) sum of zeros :-
L.H.S :-
=> alpha + beta
=> -2 + 4
=> 2
R.H.S :-
*) -- b
a
=> -- ( -2)
1
=> 2
L.H.S = R.H.S
2) Product of zeros = Constant term
Coefficient of x^2
i.e, alpha * beta = c
a
L.H.S :-
=> alpha *beta
=> (-2) (4)
=> -8
R.H.S :-
=> c
a
=> -8
1
=> -8
Thus, L.H.S = R.H.S
Hence the relationship between zeros and coefficient is verified.
*************************************************************
2) 4s^2 -- 4s +1
sol) Finding zeros :-
Let p (s) = 4s^2 - 4s +1
p (s) = 0
4s^2 - 4s +1 = 0
4s^2 - 2s - 2s +1 = 0
2s( 2s-1) - 1 (2s -1) = 0
(2s - 1 ) ( 2s - 1 ) = 0
2s-1 = 0 or 2s-1 = 0
2s=1
s=1/2 , 1/2
Therefore , alpha = 1/2 and beta = 1/2 are roots of the polynomial.
2) verifying
compare it with quadratic equation as^2 + bs + c ( 4s^2 - 4s +1)
where a = 4, b = -4, c=1
*) Sum of zeros = - Coefficient of s
Coefficient of s^2
i.e, alpha +beta = - b
a
L.H.S :-
=> alpha + beta
=> 1/2 + 1/2
=> 1
R.H.S :-
= - b
a
= - ( -4) = 4/4 = 1
4
L.H.S = R.H.S
*) Product of zeros = Constant term
Coefficient of x^2
i.e, alpha * beta = c
a
L.H.S
=> alpha * beta
=> 1/2 * 1/2
=> 1/4
R. H.S :-
=> c
a
=> 1
4
Thus, L.H.S = R.H.S
Hence relationship between zeros and coefficient is verified.
**************************************************************
3) 6x^2 -3-7x
Sol ) Rearrange in quadratic form we get 6x^2 -7x - 3
1) finding zeros :-
Let p (x) = 0
=> 6x^2 -7x - 3 = 0
=> 6x^2 +2x - 9x -3 = 0
=> 2x ( 3x +1) - 3 (3x +1) = 0
=> (3x + 1) (2x-3) = 0
=> 3x+1 = 0 and 2x-3=0
=> x= -1/3 and x= 3/2
.^. alpha = - 1/3 and beta = 3/2 are the zeros of the polynomial ( 6x^2 -7x-3)
*) verification :-
comparing with quadratic equation ax^2 + bx +c ( 6x^2 -7x-3)
where a=6, b = -7, c= -3
*) Sum of zeros = - Coeffcient of x
Coefficient of x^2
i.e, alpha + beta = - b
a
L.H.S :-
=> alpha + beta
=> -1/3 + 3/2
=> -1 *2 + 3 *3
3*2
=> -2 + 9
6
=> 7
6
R.H.S :-
=> - b
a
=> - (-7)
6
=> 7
6
L.H.S = R.H.S
*) product of zeros = constant term
coefficient of x^2
i.e , alpha * beta = c
a
L.H.S :-
=> alpha *beta
=> ( - 1 ) * (
=> - 1
2
R.H.S :-
=> c
a
=> - 3
6
=> - 1
2
Thus L.H.S = R.H.S
Hence relationship between zeros and coefficient is verified.
****************************************************************
4) 4u^2 + 8u
sol) Finding zeros :-
Let p(u) = 0
=> 4u^2 + 8 u = 0
taking "4u" common , we get.
=> 4u( u +2) = 0
=> 4u = 0 and u+2=0
=> u= 0 and u= -2
4
.^. u = 0, -2 are the zeros of the polynomial.
2) Verifying :-
When constant term is absent we can take "0"
p (u) = 4u^2 + 8 u
= 4u^2 + 8u + 0 ( Its in quadratic form au^2 +bU + c)
where a= 4, b = 8 , c= 0
*) Sum of zeros = - Coefficient of x
Coefficient of x^2
i.e, alpha +beta = - b
a
L.H.S :-
=> alpha + beta
=> 0 + ( -2)
=> 0 -2
=> -2
R.H.S :-
= > - b
a
=> - 8
4
=> -2
L.H.S = R.H.S
*) product of zeros = Constant term
coefficient of x^2
i.e, alpha * beta = c / a
L.H.S :-
=> alpha +beta
=> ( 0 ) ( -2)
=> 0
R.H.S ;-
=> c / a
=> 0 / 4
=> 0
Thus, L.H.S = R.H.S
Hence relationship between zeros and coefficient is verified.
*******************************************************
5) t^2 - 15
sol) Finding zeros :-
Let p(t) = 0
=> t^2 -15 = 0
We have formula a^2 - b^2 but t^2 - 15 is not in this form .lets make it
we can write "(-/ 15) ^2 " for 15 , we get.
=> t^2 -- ( _/ 15) ^2 ( now it is in a^2 - b^2 form)
Thus, we have => a^2 - b^2 = ( a+b) (a-b)
here a= t, and b = __/ 15,
substitute a , b value in above formula we get
=> (a+b ) (a-b) = 0
=> ( t + _/15 ) ( t - _/15 ) = 0
=> t + _/15 = 0 and t - _/ 15 = 0
= > t = - _/15 and t = _/15
.^. alpha = _/15 and beta = - _/15 are zeros of the polynomial.
2) Verifying :-
As we see the equation( t^2 - 15) is not in quadratic form ax^2+ bx + c
"bt' is missing in t^2 - 15,
we can write (t^2 + 0 (t) - 15 )
{ where "bt' = "0 (t)")
Thus, p(t) = 0
=> t^2 + 0 (t) - 15 = 0
where a= 1, b = 0 , c = -15
*) Sum of zeros = - Coefficient of x
Coefficient of x^2
i.e, alpha + beta = - b / a
L.H.S :-
=> alpha + beta
=> _/15 + ( - _/15)
=> _/15 - _/15 =0
R.H.S :-
=> - b /a
=> - 0 / 1 = 0
L.H.S = R.H.S
*) product of zeros = Constant term
coefficient of x^2
i.e, alpha * beta = c /a
L.H.S :-
=> alpha * beta
=> (_/15 ) * ( - _/15 )
= - ( _/ 15 ) ^2
= - 15
R.H.S
=> c /a
=> -15 / 1
= - 15
Thus L.H.S = R. H. S
Hence relationship between zeros and coefficient is verified.
*************************************************************
6) 3x^2 -x - 4
Sol) Finding zeros of polynomial
p(x) = 0
=> 3 x^2 - x - 4 = 0
=> 3x^2 + 3x - 4x - 4 = 0
=> 3x ( x +1) -4 (x +1) = 0
=> (x +1) ( 3x - 4) = 0
=> x +1 = 0 and 3x - 4 = 0
x= -1 and x = 4 / 3
.^. alpha = -1 , beta = 4 / 3 are zeros of polynomial.
2) verifying
ax^2 + bx + c = 3x^2 - x - 4
where a = 3, b = -1, c = -4
*) sum of zeros = - Coefficient of x
Coefficient of x^2
i.e, alpha + beta = - b / a
L.H.S :-
=> alpha + beta
=> - 1 + 4/3
=> -3 + 4
3
=> 1 / 3
R.H.S :-
=> - b / a
=> - ( -1 / 3)
= 1 / 3
*) product of zeros = constant term
coefficient of x^2
i.e, alpha * beta = c / a
L.H.S :-
=> alpha * beta
=> ( 4/ 3) * ( -1)
= -4 / 3
R.H.S :-
=> c / a
=> -4 / 3
Thus. L.H.S = R. H.S
Hence relationship between zeros and coefficient is verified.
*******************************************************
2) Find the quadratic polynomial in each case, with the given numbers as the sum and product of its zeroes respectively.
(1) 1 / 4 , - 1
Sol) we have to find the quadratic equation ax^2 + bx + c
But we have given only
1) sum of zeroes = 1 / 4 and 2) product of zeroes = - 1
As we have ,
*) sum of zeroes = coefficient of x
coefficient of x^2
we have sum of zeroes value = 1 / 4
=> 1 / 4 = - b / a
=> - b / a = 1 / 4
we can take "a" to be any real number. Let us say it is "k"
= > - b / k = 1 / 4
=> -b = 1/ 4 *k
=> b = - 1/4*k (we got "b" value)
*) product of zeroes = Constant term
Coefficient of x
we have product of zeroes value = -1
= > - 1 = c / a
assuming a = k , we get
=> c / a = -1
=> c / k = -1
=> c = -1 * k = -k ( we got " c" value )
Now we have a = k , b = - 1/ 4 k and c = -k
substitute a,b,c value in quadratic polynomial
= ax^2 + bx + c
= k * x^2 + (-1/4) k*x +(-k)
taking "k" as common we get,
= k { x^2 - 1/4 *x- 1)
we can take any real number in place of "k"
lets take "4" in place of "k"
= 4 ( x^2 -1/4 *x -1)
=4 * x^2 -
= 4x^2 - x - 4
Thus, we got the quadratic polynomial = 4x^2 -x -4
****************************************************************
2) _/2 , 1 / 3
Sol) sum of zeroes = _/2
=> - b / a = _/2
=> -b = _/2 a
lets take "k" in place of "a"
=> b = - _/2k (we got b value)
*) product of zeroes = 1 / 3
=> c / a = 1/ 3
=> c = 1 / 3 *a
=> c = (1 / 3) k ( got c value)
a=k , b = (- _/2) k , c = ( 1 / 3) k
substitute a, b, c value in quadratic equation
=> ax^2 + b x + c
=> k *x^2 + (- _/2)k *x + ( 1 /3) k
taking "k" as common
=> k { x^2 - _/2x + 1 /3 )
we can take any real number in place of "k"
lets take k = 3
= > 3 * x^2 - 3(_/2x) + 3 * 1/3
=> 3x^2 - 3_/2x + 1
Thus, we got quadratic polynomial 3x^2 - 3_/2x + 1
*******************************************************************
3) 0, _/5
sol) sum of zeroes = 0
=> - b / a = 0
=> -b = 0
=> b = 0 ( got "b" value" )
*) product of zeroes = _/5
=> c / a = _/5
=> c = _/5 * a
let a=k
=> c = _/5k ( got "c" value)
we have a =k, b = 0 , c = _/5k
substitute a,b,c value in quadratic equation "
=> ax^2 +bx+c
=> k*x^2 + 0*x + _/5k
=> kx^2 + 0x + _/5k
we can take any real no. value for "k"
lets take k=1 , we get
=> 1x^2 + 0x + _/5
Thus we got
quadratic polynomial = 1x^2 +0x + _/5 or x^2 + _/5
***********************************************
(4) 1, 1
sol) sum of zeroes = 1
=> - b / a = 1
=> - b = 1 *a
=> - b = a
=> b= -a
let a = k
=> b = -k
*) product of zeroes = 1
=> c / a = 1
=> c = a
take a= k
=> c = k
substitute a,b,c value in
=> ax^2+bx+c
=> kx^2 + (-k)x + k
can take any real number value in place of "k"
lets take k=1, we get
=> 1.x^2 + (-1)x +1
=> x^2 -x +1
Thus it's in quadratic form ax^2 + bx = c
Hence, the required quadratic polynomial = x^2 - x +1
********************************************************
5) - 1/4 , 1/4
sol) sum of zeros = - 1/4
- b/a = -1/4
put a =k , we get
=> -b / k = -1/4
=> -b = -1/4 *k
=> b= (1/4)k ( got "b" value)
*) product of zeroes = 1/4
=> c/a = 1/4
let a=k , we get
=> c /k = 1/4
=> c= (1/4) k
substitute a,b,c value in quadratic equation ax^2 + bx+c
a= k, b = (1/4)k, c= (1/4)k
we get,
=> k x^2 + (1/4)k*x + (1/4)k
put k =4, we get
=> 4 * x^2 + ( 1/4 *4) x + ( 1/4*4)
( 1/4*4 = 1)
=> 4x^2 + 1x +1
Hence, the required quadratic polynomial = 4x^2 =x+1
*************************************************************
6) 4 , 1
sol) Sum of zeroes = 4
=> -b/a = 4
take a=k
=> -b/k = 4
=> -b = 4k
=> b = -4k ( got "b" value)
*) product of zeroes = 1
=> c /a = 1
let a=k , we get
=> c/k = 1
=> c = k
Substitute a,b,c we get
where a =k, b = -4k, c= k
=> ax^2 +bx+c
=> kx^2 + (-4k)x + k
put k=1
=> x^2 - 4x =1 is the required polynomial.
***********************************************************************
3) Find the quadratic polynomial, for the zeroes alpha,beta given in each case.
(1) 2, -1
sol) Let the quadratic polynomial be ax^2 +bx+c and its zeroes be 2,-1
we have alpha =2, beta = -1
=> Sum of Zeroes :-
alpha +beta = 2 + (-1) =2-1 =1
=> product of zeroes :-
alpha *beta = 2 * (-1) = -2
.^. the quadratic polynomial ax^2 + bx +c is
(*) Formula :-
k [ x^2 - ( alpha + beta) x + (alpha *beta)],
where "k" is constant
=> k [ x^2 + (-1) x + (-2) ]
We can put different value of "k"
When k=1
The quadratic polynomial will be x^2-x -2
********************************************************
(2) _/3 , -_/3
sol) let the quadratic polynomial be ax^2 +bx +c and its zeroes be _/3, -_/3
We have ,
alpha = _/3
beta = -_/3
=> Sum of zeroes :-
Alpha + beta = _/3 + (-_/3) = _/3 - _/3 = 0
=> product of zeroes :-
alpha * beta = _/3 * (-_/3) = -3
.^. the quadratic polynomial ax^2+bx+c is
(*) Formula :-
=> k [ x^2 - ( alpha +beta ) x + ( alpha *beta)]
where "k" is constant
substitute , ( alpha +beta) = 0 and (alpha * beta) = -3 in above formula
we get,
=> k [ x^2 - (0)x + 3) ]
We can take different value for "k"
When k=1
=> 1[ x^2 - 0x +3]
=> x^2 - 3
the quadratic polynomial will be x^2 - 3
*************************************************************
3) 1 / 4 , -1
sol) let the quadratic polynomial be ax^2 +bx+c and its zeroes be 1/4, -1
We have,
alpha = 1/ 4
beta = -1
=> sum of zeroes :-
alpha +beta
= 1 / 4 + (-1)
= 1 / 4 -1
= 1 - 4
4
= - 3/ 4
=> product of zeroes :-
alpha * beta
= 1 / 4 * (-1)
= - 1/4
.^. the quadratic polynomial ax^2+bx+c is
(*) Formula :-
=> k { x^2 - ( alpha + beta) x + (alpha *beta) ]
where "k" is constant
substitute (alpha +beta) = -3/4 and (alpha*beta) = -1/4 in above formula
We get,
=> k [ x^2 - ( -3/4) x + ( -1/4) ]
We can take different value for "k"
when k= 4
=> 4 [x^2 - (-3/4) x + (-1/4) ]
=> 4x^2 + (4*3/4) x - (4*1/4)
( 4*3/4 = 3 and 4*1/4=1)
=> 4x^2 +3x -1
The quadratic polynomial will be 4x^2 +3x -1
*****************************************************
4) 1/2 , 3/2
sol) let the quadratic polynomial be ax^2+bx+c , and its zeroes be
alpha = 1/2
beta = 3/2
(*) Sum of zeroes :-
alpha + beta
=. 1/2 + 3/2
= 1+3
2
= 4 /2 = 2
(*) products of zeroes :-
alpha * beta
=> 1/2 * 3/2
=> 3/4
.^. the quadratic polynomial ax^2+bx+c is
(*) Formula ;-
=> k [ x^2 - ( alpha +beta ) x + ( alpha *beta) ]
substitute (alpha +beta ) = 2 and (alpha *beta) = 3/4 in above formula
We get,
=> k [ x^2 - ( 2) x + (3/4) ]
take k= 4, we get
= 4 [ x^2 -2x +3/4]
= 4x^2 - 8x + 4(3/4)
=4x^2 - 8x +3
( 4 *3/4 = 3)
Thus the quadratic polynomial will be 4x^2-8x+3
******************************************************
4) verify that 1, -1 and -3 are the zeroes of the cubic polynomial x^3 + 3x^2 -x - 3 and check the relationship between zeroes and the coefficients.
sol) comparing the given polynomial
x^3 + 3x^2-x-3 = ax^3 + bx^2 + cx +d ,
we get, a= 1 , b= 3, c=-1 , d= -3.
Further
(*) verifying zeroes 1, -1, and -3 of this cubical polynomial:-
p (1) = 1^3 + 3(1)^2 - (1) - 3
= 1+3 -1 -3
= 0
p(-1) = (-1)^3 + 3 (-1)^2 - (-1) -3
= -1 +3 +1 -3
= 0
p(-3) = ( -3)^3 + 3 (-3)^2 - (-3) - 3
= -27 + 27 +3 -3
= 0
.^. 1, -1, and -3 are the zeroes of x^3 +3x^2-x-3
So, we take alpha = 1, beta= -1 , gamma = 3
now, for a cubic polynomial p(x) = ax^3 + b x^2 +cx+d
with zeroes alpha, beta and gamma
we have
1)
sol) 1 + (-1) + (-3)
= 1-1-3
= -3 or -3/1
= -b / a
(2)
sol) 1(-1) + (-1)(3) + (3) (1)
= -1 -3 +3
= -1 or -1/1
= c / a
(3)
sol ) (1) (-1) (3)
= -3 or -3/1
= -d / a
Hence , the relationship is verified.
********************************************************
(*) Division Algorithm for polynomials
We know cubic polynomial has at most three zeroes.
However, if you are given only one zero, can you find the other two?
Let us consider the cubic polynomial
x^3 + 3x^2 - x - 3.
If we tell you that one of its zeroes is 1, then you know that this polynomial is divisible by x-1.
Dividing by x-1 we would get the quotient
x^2 - 2x - 3.
We get the factors of x^2 - 2x - 3 by splitting the middle term. The factors are (x+1) and (x-3). This gives us
x^3 + 3 x^2 - x - 3 = (x-1)(x^2 - 2x- 3)
= (x-1)(x+1)(x-3)
So, the three zeroes of the cubic polynomial are
1,-1,3.
*****************************************
Example-8. Divide 2x^2 + 3x + 1 by x +2
sol). Note that we stop the division process when either the remainder is zero or its degree is less than the degree of the divisor .
So, here the Quotient is 2x-1 and the remainder is 3. Also.
(2x-1)(x+2) +3 = 2x^2 +3x-2 +3
=> 2x^2 + 3x + 1
i.e., 2x^2 + 3x + 1 = (x+2)(2x-1) + 3
Therefore ,
Dividend = Divisor * Quotient + Remainder
*****************************************
Example-9. Divide 3x^3 + x^2 + 2x + 5 by
1 + 2x + x^2
sol) We first arrange the terms of the dividend and the divisor in the decreasing order of their degrees.
Arranging the terms in this order is termed as writing the polynomials in its standard form.
In this example, the dividend is already in its standard form, and the divisor, also in standard form, is x^2 + 2x + 1.
Step 1 : To obtain the first term of the quotient, divide the highest degree term of the dividend (i.e., 3x^3) by the highest degree term of the divisor (i.e., x^2). This is 3x.
Then carry out the division process. What remains is -5x^2-x+5.
Step 2. Now, to obtain the second term of the quotient, divide the highest degree term of the new dividend (i.e. -5x^2) by the highest degree term of the divisor (i.e., x^2).
This gives -5. Again carry out the division process with -5x^2-x+5.
Step 3. What remains is 9x+10. Now, the degree of 9x+10 is less than the degree of the divisor x^2+2x+1. So, we cannot continue the division any further.
So, the quotient is 3x-5 and the remainder is
9x + 10. Also
= (x^2+2x+1)*(3x-5)+(9x+10)
= (3x^3 + 6x^2 + 3x - 5x^2 - 10x - 5 + 9x + 10)
= 3x^3 + x^2 + 2x + 5
Here again, we see that
Dividend = Divisor* Quotient+ Remainder
We are applying here an algorithm called Euclid's division algorithm
This says that
If p(x) and g(x) are any two polynomials with g(x)=/=0, then we can find polynomials q(x) and r(x) such that
p(x) = g(x)*q(x)+r(x),
where either r(x)=0 or degree of
r(x)<degree of g(x) if r(x) =/= 0
This result is known as the Division Algorithm for polynomials.
Now, we have the following results from the above discussions.
(!) If q(x) is linear polynomial then r(x) = r is a constant.
(!!) If degree of q(x) = 1 , then degree of p(x) = 1 + degree of g(x).
(!!!) If p(x) is divided by (x-a), then the remainder is p(a).
(!v) If r = 0, we say q(x) divides p(x) exactly or q(x) is a factor of p(x).
*****************************************
Example-10. Divide 3x^2-x^3-3x+5 by x-1-x^2, and verify the division algorithm.
sol) Note that the given polynomials are not in standard form.
To carry out division, we first write both the dividend and divisor in decreasing orders of their degrees.
So,
dividend = -x^3 + 3x^2 - 3x+5 and
divisor = -x^2 +x-1.
We stop here since degree of the remainder is less than the degree of (-x^2+x-1) the divisor.
So,
quotient = x-2, remainder = 3.
Now,
Dividend = Divisor * Quotient + remainder
= (-x^2 +x-1) * (x-2) + 3
= -x^3 + x^2 - x +2x^2-2x+2+3
= -x^3 + 3x^2 - 3x + 5
In this way, the division algorithm is verified.
*****************************************
Example-11. Find all the zeroes of
2x^4 -3x^3 - 3x^2 + 6x - 2 are √2 and - √2
sol) Since two of the zeroes are √2 and -√2, therefore we can divide by
(x-√2) (x+√2) = x^2 - 2.
So,
2x^4 - 3x^3 + 6x - 2
=(x^2 - 2) (2x^2 - 3x + 1).
Now, by splitting -3x, we factorize
2x^2-3x+1
2x^2 -2x-x+1
2x(x-1) -1(x-1)
(2x-1)(x-1).
So, its zeroes are given by
x = 1/2 and x = 1.
Therefore, the zeroes of the given polynomial are
√2, -√ 2, 1 and 1/2
*****************************************
(*) Exercise - 3.4
1) Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following :
(1) p (x) = x^3 -3x^2 +5x - 3, g(x) = x^2 - 2
sol)
Quotient = ( x-3)
remainder = ( 7x -9)
------------------------------------------------------------------------------------------
(2) p(x) = x^4 - 3x^2 +4x +5, g(x) = x^2+1-x
sol)
Quotient : x^2 +x -3
Remainder = 8
-------------------------------------------------------------------------------------
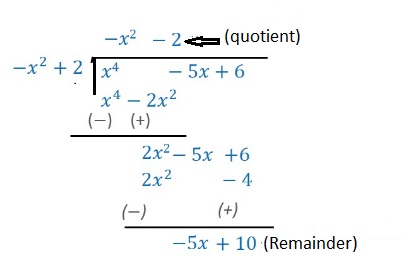
3) p (x) = x^4 -5x +6 , g(x) = 2 - x^2
sol) Note that the given polynomial g(x) = 2 - x^2 are not in standard form. To carry out division, we first write divisor ( 2 - x^2) in decreasing orders of their degrees.
so, divisor = 2 - x^2 = = - x^2 + 2
Quotient = -x^2 - 2
Remainder = -5x +10
**************************************************************
2) Check in which case the first polynomial is a factor of the second polynomial by divising the second polynomial by the first polynomial.
(1) (first poly)= t^3 -3 , (2nd poly)= 2t^4+3t^3-2t^2 - 9t - 12
sol)
Since the remainder is "0"
Hence, t^3 - 3 is a factor of 2t^4 + 3t^3 -2t^2 -9t -12
-------------------------------------------------------------------------------------------
(2) (1st poly) = x^2 +3x +1 (2nd poly) = 3x^4 +5x^3 - 7x^2 +2x+2
sol)
Since the remainder is "0"
Hence , x^2 +3x +1 is a factor of 3x^4 + 5x^3 -7x^2 +2x +2
----------------------------------------------------------------------------
(3) (1st poly) = x^3 - 3x +1, (2nd poly) = x^5 -4x^3 +x^2+3x+1
sol
Since the remainder is NOT "0"
Hence , x^3 - 3x + 1 is not a factor of x^5 - 4x^3 +x^2 + 3x +1
*****************************************************
3) obtain all other zeroes of 3x^4 + 6x^3 - 2x^2 - 10x - 5, if two of its zeroes are
sol) let p(x) = 3x^4 + 6x^3 - 2x^2 - 10x - 5
Since
by ( x^2 - 5/3) we can find out the other factors.
Now, we factorize ,
=> 3x^2 + 6x + 3
=> 3x^2 + 3x +3x +3
=> ( 3x^2 +3x) + (3x +3)
=> 3x( x +1) + 3 (x+1)
=> (3x+3) (x+1)
=> 3x+3 = 0 and x+1=0
=> 3x = -3 and x =-1
=> x= -1 , -1 also zero of p(x)
.^. , the other zeroes of p(x) are -1, -1
*******************************************************
4) On dividing x^3 - 3x^2 +x +2 by a polynomial g(x), the quotient and remainder were (x-2) and (-2x +4), respectively , Find g(x).
sol) We have a formula
Dividend = Divisor * Quotient + Remainder
Given,
p(x) = x^3 -3x^2 +x+2 ( dividend)
g(x) = ? ( Divisor)
Quotient = ( x-2)
Remainder = ( -2x +4)
Using the above formula we get,
=> x^3 -3x^2 + x +2 = g (x) * (x-2) + ( -2x +4)
Transfer (-2x +4) to left side we get
=> x^3 -3x^2 +x+2 +2x- 4 = g (x) * (x-2)
=> x^3 -3x^2 +3x - 2 = g (x) * (x-2)
=> x^3 -3x^2 +x+2 = g(x)
(x-2)
Lets divide to get g(x)
We get,
.^. g (x) = x^2 -x-1
***************************************
5) Give examples of polynomials p (x) , g (x) , q(x) and r (x), which satisfy the division algorithm
(1) deg p(x) = deg q(x) [ degree=deg]
sol) We have to find p(x) , g(x), q(x) & r(x)
p(x) = dividend
g(x) = divisor
q(x) = Quotient
r(x) = Remainder
let us assume g(x) to be a small number g(x) = 4
and let p(x) = 4x +8
q(x) = x+2
r (x) = 0
Deg p(x) = 1
Deg q(x) = 1
.^. deg p(x) = deg q(x)
--------------------------------------------------------------------------------------
2) deg q(x) = deg r (x)
sol) let p (x) = 2x^2 + 6 , g(x) = 2x + 2
q(x) = x
r(x) = -2x +6
Deg of q (x) = 1
Deg of r (x) = 1
.^. deg q (x) = deg r(x)
--------------------------------------------------------------------------
(3) deg r(x) = 0
Sol) let p (x) = 4x +8, g (x) = 4
so, q(x) = x +2
r (x) = 0
.^. Deg r(x) = 0
*******************************************************************
(*) optional exercise
1. verify that the numbers given alongside the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and the coefficients in each case :
(!) 2x^3 + x^2 - 5x + 2; (1/2, 1, -2)
sol) Let p(x) = 2x^3 + x^2 - 5x + 2
Verifying zeroes:-
When x = 1/2
p(1/2) = 2(1/2)^3 + (1/2)^2 - 5(1/2) + 2
= 1 + 1 - 5 + 2
4 4 2
= 1 + 1 -10 + 8
4
= 0/4 = 0
Hence, (1/2) is a zero of p(x)
*****************************************
when x = 1
p(1) = 2(1)^3 + (1)^2 - 5(1) + 2
= 2 + 1 - 5 + 2
= 5 - 5
p(1)= 0
Hence, 1 is a zero of P(x)
******************************************
At x= -2
p(-2) = 2(-2)^3 + (-2)^2 -5(-2) + 2
= -16 + 4 +10 + 2
= -16 + 16 = 0
p(-2) = 0
Hence, -2 is a zero of p(x)
Verifying relationship between zeroes and coefficients :
For a cubic polynomial
p(x) = ax^3 + bx^2 + cx + d
with zeroes 𝝰,𝛃 and 𝜸
we have
𝝰 + 𝛃 +𝜸 = -b/a
𝝰𝛃 + 𝛃𝜸 + 𝜸𝝰 = c/a
𝝰𝛃𝜸 = -d/a
For p(x) = 2x^3 + x^2 - 5x + 2
a =2
b=1
c = -5
d = 2
𝝰= 1/2 , 𝛃=1, and 𝜸=-2
𝝰 + 𝛃 +𝜸 = -b/a
1/2 + 1 - 2 = -1/2
1 - 2 = -1/2
2
-1/2 = -1/2
1/2 = 1/2
𝝰𝛃 + 𝛃𝜸 + 𝜸𝝰 = c/a
(1/2*1) + (1*2) + (-2*1/2) = -5/2
1/2 - 2 -1 = -5/2
1/2 - 3 = -5/2
-5/2 = -5/2
(*) 𝝰𝛃𝜸 = -d/a
(1/2 * 1 * -2) = -2/2
-2/2 = -2/2
1 = 1
Thus, the relationship between zeroes and the coefficients are verified.
******************************************
(!!) x^3 - 4x^2 + 5x - 2; (2,1,1)
sol) p(2) = (2)^3 - 4(2)^2 + 5(2) - 2
= 8 - 16 + 10 - 2 = 0
p(1) = (1)^3 - 4(1)^2 + 5(1) - 2
= 1 - 4 + 5 -2
= 0
p (1) = (1)^3 - 4 (1)^2 + 5 (1) - 2
= 1 - 4 + 5 -2
= 0
Thus, 2,1,1 are the zeroes of the given polynomial.
comparing the given polynomial with
ax^3 + bx^2 + cx + d
we get,
a = 1
b = -4
c = 5
d = -2
Also, 𝜶 = 2, 𝛃=1, 𝜸=1
Now,
𝝰 + 𝛃 +𝜸 = -b/a
2 + 1 + 1 = -(-4)/1
4 = 4.
𝝰𝛃 + 𝛃𝜸 + 𝜸𝝰 = c/a
(2*1) + (1*1) + (1*2) = 5/1
2 + 1 + 2 = 5
5=5
𝝰𝛃𝜸 = -d/a
(2*1*1) = 2/1
2 = 2
Thus, the relationship between zeroes and the coefficients are verified.
******************************************
2). Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, -7, -14 respectively.
sol) For a cubic polynomial
p(x) = ax^3 + bx^2 + cx + d
with zeroes 𝝰,𝛃 and 𝜸
we have
sum= 𝝰 + 𝛃 +𝜸(2) = -b/a
sum of the product of its zeroes taken two at a time. = 𝝰𝛃 + 𝛃𝜸 + 𝜸𝝰(-7) = c/a
product of its zeroes = 𝝰𝛃𝜸(-14) = -d/a
(*) Sum of zeroes = 2
-b/a = 2
Assuming a = 1
-b/1 = 2
b = -2
(*) sum of product of zeroes = -7
c/a = -7
c/1 = -7
c = -7
(*) Product of zeroes = -14
d/a = -14
-d/1 = -14
d = 14
Thus,
a = 1, b = -2, c = -7 c = 14
Hence,
p(x) = ax^3 + bx^2 + cx + d
= (1)*x^3 + (-2)*x^2 + (-7)*x +14
= x^3 - 2x^2 - 7x + 14
*****************************************
3). If the zeroes of the polynomial x^3 - 3x^2 +x + 1 are a-b, a , a+b find a and b.
sol) Given : P(x) = x^3 - 3x^2 + x + 1
a = 1, b = -3
c = 1 d = 1
zeroes of polynomial :
𝜶 = a-b
𝛃 = a
𝜸 = a+b
(*) sum of zeroes :
𝝰 + 𝛃 + 𝜸 = -b/a
(a-b) + a + (a+b) = -(-3)/1
3a = 3
a = 1
(*) product of zeroes :
𝜶𝛃𝜸 = -d/a = -1/1 = -1
(a-b)*a*(a+b) = -1
(a^2 - b^2) * a = -1
a^3 - b^3 = -1
(1)^3 - b^2 = -1
-b^2 = -1-1 = -2
b^2 = 2
b = +√2
Thus,
a = 1 and b = +√2
******************************************
4) If two zeroes of the polynomial x^4 - 6x^3 - 26x^2 + 138x - 35 are 2+√3, find other zeroes.
sol) Given:- zeroes of polynomial are
x = 2 + √3 and x = 2 - √3
x - 2 - √3 = 0 is a factor and
x - 2 + √3 = 0 is a factor
[(x-2)-√3)] * [( x-2) + √3)] is also a factor
*********************************
(a -b ) * (a + b) = a^2 - b^2 form
*********************************
(x-2)^2 - (√3)^2
x^2 + 4 -4x - 3
.^. x^2 - 4x + 1 is a factor of
p(x) = x^4 -6x^3 - 26x^2 + 138x - 35
Now by dividing p(x) by (x^2 -4x+1)
we can find out other factors
now,
we find zeroes of
x^2 - 2x - 35 = 0
x^2 - 7x + 5x - 35 = 0
x(x-7) + 5(x - 7) = 0
(x+5)(x-7) = 0
so x = -5, and x = 7
.^., the zeroes of p(x) are
2+√3, 2 -√3, - 5 and 7
******************************************
5). If the polynomial x^4 - 6x^3 - 16x^2 + 25x + 10 is divided by another polynomial x^2 - 2x + k, the remainder comes out to be x+a, find k and a.
sol) Given : Remainder = x+a
Let p(x) = x^4 - 6x^3 - 16x^2 + 25x + 10
Let q(x) = x^2 - 2x + k
Lets divide p(x) by q(x)
Thus,
Remainder = -9x + 2kx + 10 - 8k + k^2
(2k - 9)x + k(k-8) + 10
But given remainder = x+ a
Therefore, equating both remainders
we get
(2k-9)x + k(k-8) + 10 = x + a
Now, comparing value of x terms,we get
(2k - 9)x = x
2k - 9 = 1
2k = 10
k = 5
comparing the remaining
k(k-8) + 10 = a
put k = 5 in above
5(5-8) + 10 = a
5*(-3)+ 10 = a
-15+ 10 = a
-5 = a
.^. k = 5 and a = -5




























































No comments:
Post a Comment