(*) Naming the sides in a right Triangle
Let's take a right triangle ABC as shown in the figure.
In triangle ABC, we can consider ∠CAB as A is an acute angle. Since AC is the longest side, it is called " hypotenuse"
Here you observe the position of side BC with respect to angle A. It is opposite to angle A and we can call it as "opposite side of angle A". And the remaining side AB can be called as " Adjacent side of angle A"
AC = Hypotenuse
BC = Opposite side of angle A
AB = Adjacent side of angle A
(*) Ratios in a Right Angle Triangle:
Consider a right angle triangle ABC having right angle at B
Then, trigonometric ratios of the angle A in right angle triangle ABC are defined as follows:
Sine of ∠A :
sinA=Length of the side opposite to angle A
Length of hypotenuse
= BC
AC
(*) Cosine of ∠A
cosA=Length of the side adjacent to angle A
length of hypotenuse
= AB
AC
(*) Tangent of ∠A
TanA=Length of the side opposite to angle A
Length of the side adjacent to angle A
= BC
AB
(*) Multiplicative inverse :-
Multiplicative inverse of "sine A" is "cosecant A".
simply written as " cosec A"
i.e., cosec A = 1
sin A
Similarly,
Multiplicative inverse of "cos A" is "secant A"(simply written as "sec A") and that of "Tan A" is cotangent A (simply written as cot A)
i.e., sec A = 1
cos A
and
cot A = 1
Tan A
How can you define 'cosec' in terms of sides?
If
sin A = Opposite side of the angle A
Hypotenuse
then
cosec A = Hypotenuse
Opposite side of the angle A
*****************************************
Example-1. If Tan A = 3/4, then find the other trigonometric ratio of angle A.
sol) Tan A = Opposite side = 3
Adjacent side 4
.^., opposite side : adjacent side = 3:4
For angle A,
opposite side = BC=3k
Adjacent side =AB=4k(where k is any +ve no)
Now, we have in triangle ABC( by Pythagoras theorem)
AC^2 = AB^2 + BC^2
=>(3k)^2 + (4k)^2 = 25k^2
AC = √25k^2
=> 5k = Hypotenuse
Now,we can easily write the other ratios of trigonometry
sin A = 3k = 3
5k 5
cos A = 4k = 4
5k 5
cosec A = 1 = 5
sin A 3
sec A = 1 = 5
cos A 4
cot A = 1 = 4
tan A 3
****************************************
Example-2. if ∠A and ∠P are acute angles such that sin A= sin P then prove that ∠A = ∠P
Sol) Given sin A = sin P
we have
sin A = BC
AC
sin P = QR
PQ
Then BC = QR
AC PQ
.^., BC = QR = k ----------(1)
AC PQ
By using Pythagoras theorem
AB = √AC^2 - BC^2
PR √PQ^2 - QR^2
AB = √AC^2 - k^2 AC^2 (from (1)
PR √PQ^2 - k^2 PQ^2
AB = √AC^2
PR √ PQ^2
AB = AC = BC
PR PQ QR
then
△ABC ~ △PQR
Therefore, ∠A = ∠P
*****************************************
Example-3. Consider a triangle PQR, right angled at P, in which PQ= 29 units, QR=21 units and ∠PQR = 𝜽, then find the values of
(!) cos^2 𝜽 + sin^2 𝜽
sol)In PQR, we have
PR = √PQ^2 - QR^2
= √(29)^2 - (21)^2
=√400 = 20 units
sin 𝜽 = PR = 20
PQ 29
cos 𝜽 = QR = 21
PQ 29
Now
(!) cos^2 𝜽 + sin^2 𝜽
sol) = (20)^2 + (21)^2
(29)^2 (29)^2
= 221 + 400 = 1
841
(!!) cos^2 𝜽 - sin^2 𝜽
sol) (20)^2 - (21)^2
(29)^2 (29)^2
= - 41
841
****************************************
Exercise - 11.1
(1) In right angle triangle ABC 8 cm, 15cm and 17 cm are the lengths of a AB, BC and CA respectively. Then, find out sin A, cos A and tan A.
sol)
(a) sin A= Length of the side opposite to angle A
Length of hypotenuse
=> 15
17
(b) CosA= Length of the side adjacent to angle A
Length of hypotenuse
=> 8
17
(c) tanA = Length of the side opposite to angle A
Length of the side adjacent to angle A
=> 15
8
**********************************************
(2) The sides of a right angle triangle PQR are PQ = 7 cm, QR = 25 cm and ∠ Q = 90 deg respectively. Then find tanQ - tan R.
sol)
In PQR, we have
By Pythagoras theorem :-
PR^2 = PQ^2 + QR^2
PR^2 = (7)^2 + (24)^2
PR^2 = 49 + 576
PR^2 = 625
PR = _/ 625
PR = 25
Now we have,
PQ = 7 cm, QR = 25 cm and PR = 25 cm
(a) tanP =Length of the side opposite to angle P
Length of the side adjacent to angle P
=> 24
7
(b) tanR=Length of the side opposite to angle R
Length of the side adjacent to angle R
=> 7
24
Now,
(c) tanP -- tanR
=> 24 -- 7
7 24
=> 576 -- 49
168
=> 527
168
=> 3.13
************************************************
(3) In a right angle triangle ABC with right angle at B, in which a = 24 units units, b = 25 units and /_BAC =
sol) In /_\ ABC, we have
BC = a = 24 units
AC = b = 25 units
/_BAC =
By Pythagoras theorem :-
AC^2 = AB^2 + BC^2
(25)^2 = AB^2 + (24)^2
AB^2 = (25)^2 - (24)^2
AB^2 = 625 - 576
AB^2 = 49
AB = _/49
AB = 7 units
(a) cos
=> AB
AC
=> 7
25
=> 0.28 units
(b) tan
Length of the side adjacent to angle
AB
=> 24
7
=> 3.42 units
*******************************************
(4) If cos A = 12 / 13, then find sin A and tan A
sol) We know that,
Cos A = Adjacent side
Hypotenuse
Cos A = 12
13
using Pythagoras Theorem :-
(Hypotenuse)^2 = (opposite )^2 + (adjacent)^2
(13)^2 = (opposite)^2 + (12)^2
(13)^2 - (12)^2 = (opposite)^2
169 - 144 = (opposite)^2
25 = (Opposite)^2
_/25 = opposite
5 = opposite
Now we have ,
opposite = 5 units
adjacent = 12 units
Hypotenuse = 13 units
So,
(a) Sin A = Opposite side = 5
Hypotenuse 13
(b) Tan A = Opposite side = 5
Adjacent side 12
*******************************
(5) If 3 tan A = 4, then find sin A and cos A.
sol) Given :- 3 tan A = 4
=> tan A = 4 = opposite side
3 adjacent side
opposite side = 4
adjacent side = 3
hypotenuse =?
Using Pythagoras theorem :-
(hypotenuse)^2 = ( opposite)^2 + ( adjacent side)^2
(hypotenuse)^2 = ( 4 )^2 + (3)^2
(hypotenuse)^2 = 16 + 9
( hypotenuse)^2 = 25
hypotenuse = _/25
hypotenuse = 5 units
Now,
(a) Sin A = opposite side = 4
hypotenuse 5
(b) Cos A = adjacent side = 3
hypotenuse 5
*************************************
(6) If /_A and /_X are acute angles such that cos A = cos X then show that /_A = /_X.
sol) We know
cos A = adjacent
hypoten
=> AC
AX -----(1)
Cos X = adjacent
hypotenuse
=> CX
AX --------(2)
Given :- Cos A = Cos X
=> AC = CX
=> AC = XC
We know
Angles opposite to equal sides of a triangle are equal.
/_ A = /_ X
Hence proved
**********************************************
(7) Given cot 0 = 7/8, then evaluate
(1) ( 1 + sin
( 1 + cos
sol) Given :- cot
opposite side
adjacent side = 7
opposite side = 8
(Hyp)^2 = (oppo)^2 + (adja)^2
" = ( 8)^2 + ( 7)^2
" = 64 + 49
(Hyp)^2 = 113
(Hyp) = _/113
Now,
Sin
Hypotenuse _/113
Cos
Hypotenuse _/113
(1 + sin
(1 + cos
**************************
Using (a +b) (a-b) = a^2 - b^2
***************************
=> (1^2 - sin^2
( 1^2 - cos^2
=> (1 - ( 8 )^2 )
_/113
( 1 - ( 7 ) ^2 )
_/113
=> ( 1 - 64 )
113
( 1 - 49 )
113
=> ( 113 - 64 )
113
( 113 - 49 )
113
=> 113 - 64
113 - 49
=> 49
64
*****************************
(2) ( 1 + sin
cos
-/113
7
_/113
=> ( _/113 + 8)
_/113
7
_/113
=> ( _/113 + 8)
7
********************************
(8) In a right angle triangle ABC , right angle is at "B" , if tan A = _/3 then find the value of
(1) Sin A Cos C + Cos A Sin C
sol) Given :- Tan A = _/3 = opposite side
1 adjacent side
(Hyp)^2 = ( Oppo)^2 + (adja)^2
" = (_/3)^2 + ( 1 )^2 )
" = ( 3 + 1)
(Hyp) = _/4 = 2
Now we got
Opposite side = _/3
Adjacent side = 1
Hypotenuse = 2
Now,
Sin A = side Opposite to angle A = _/3 / 2
Hypotenuse
Sin C = side opposite to angle C = 1 / 2
Hypotenuse
Cos A = side adjacent to angle A = 1 / 2
Hypotenuse
Cos C = adjacent to angle C = _/3 / 2
Hypotenuse
Now
(a) Sin A Cos C + Cos A Sin C
sol) _/3 * _/3 + 1 * 1
2 2 2 2
=> 3 + 1
4 4
=> 4 / 4 = 1
*******************
sol) 1 * _/3 -- _/3 * 1
2 2 2 2
=> _/3 / 4 - _/3 / 4
=> 0
*********************************************************************************
(*) Trigonometric ratios
Example-4. In ABC, right angle is at B, AB=5cm and ∠ACB = 30 deg. determine the lengths of the sides BC and AC.
Sol) Given AB=5 cm and ∠ACB = 30 deg.
To find the length of side BC, we will choose the trignometric ratio involving BC and the given side AB.
Since BC is the side adjacent to angle C and AB is the side opposite to angle C.
Therefore,
AB = Tan C
BC
i.e, 5 = Tan 30 deg = 1
BC √3
Which gives BC = 5√3 cm
Now, by using the Pythagoras theorem
AC^2 = AB^2 + BC^2
AC^2 = (5)^2 + (5√3)^2
AC^2 = 25 + 75
AC = √ 100 = 10 cm.
*****************************************
Example-5. A chord of a circle of radius 6cm is making an angle 60 deg at the center. Find the length of the chord.
sol) Given the radius of the circle OA=OB=6cm
∠AOB = 60 deg
OC is height from 'O' upon AB and it is a angle bisector.
then,∠COB = 30 deg
Consider △COB
sin 30 = BC
OB
1 = BC
2 6
BC = 6/2 = 3
But, length of the chord AB=2BC
=> 2 *3 = 6 cm
Therefore, length of the chord = 6 cm.
*****************************************
Do you know?
The first use of the idea of 'sine' in the way we use it today was in the book Aryabhatiyam by Aryabhatta, in A.D. 500.
Aryabhatta used the word ardhajya for the half-chord, which was shortened to jya or jiva in due course.
When the Aryabhatiyam was translated into Arabic, the word jiva was retained as it is.
The word jiva was translated into sinus, which means curve, when the Arabic version was translated into Latin. Soon the word sinus, also used as sine, become common in mathematical texts throughout Europe.
An English Professor of astronomy Edmund Gunter(1581-1626) first used the abbreviated notation 'sin'.
****************************************
Example-6. In △PQR, right angle is at Q, PQ= 3 cm and PR = 6 cm. determine ∠QPR and ∠PRQ
sol) Given PQ = 3 cm and PR = 6 cm
Therefore, PQ = sin R
PR
or sin R = 3 = 1
6 2
So,∠PRQ = 30 deg
and therefore,∠QPR = 60 deg
NOTE: If one of the sides and any other part(either an acute angle or any side) of a right angle triangle is known, the remaining sides and angles of the triangle can be determined.
*****************************************
Example-7, If sin(A - B) = 1/2, cos(A+B) = 1/2,
0<A+B< 90, A>B, find A and B.
sol) Since sin(A-B) = 1/2
.^., A - B = 30 deg
Also,
since cos(A+B) = 1/2,
.^., A+B = 60 deg
Solving the above two equations, we get
A = 45 deg
B = 15 deg
*****************************************
Exercise - 11.2
(1) Evaluate the following.
(1) sin 45 deg + cos 45 deg
sol) 1 + 1
_/2 _/2
******************************
sin 45 deg == cos 45 deg == 1 / _/2
******************************
=> 2
_/2
=> _/2 *
*****************
_/2 * _/2 = 2
****************
=> _/2 = sin 45 deg + cos 45 deg
******************************
(2) cos 45 deg
sec 30 deg + cosec 60
sol) 1 / _/2
----------------------
2 / _/3 + 2/_/3
************************
sec 30 deg = 2 / _/3
cosec 60 deg = 2/ _/3
*************************
=> 1 / _/2
-------------
4 / _/3
=> _/3
--------
4 _/2
***********************************
(3) sin 30 deg + tan 45 deg - cosec 60 deg
cot 45 deg + cos 60 deg - sec 30 deg
sol)
--------------------------------------
=> 1
******************************
(4) 2 tan^2 45 deg + cos^2 30 deg - sin^2 60 deg
sol) 2 (1)^2 + (_/3)^2 - (_/3)^2
2 2
=> 2 + 3/4 -- 3/4
=> 2
***************************
(5) sec^2 60 deg - tan^2 60 deg
sin^2 30 deg + cos^2 30 deg
sol) (2)^2 - (_/3)^2
--------------------
(1/2)^2 + ( _/3 /2)^2
=> 4 - 3
(1/4 + 3/4 )
=> 1
(4/4)
=> 1
****************************
2) Choose the right option and justify your choice -
(1) 2 tan 30 deg
1 + tan^2 45 deg
(a) sin 60 deg
(b) cos 60 deg
(c) tan 30 deg
(d) sin 30 deg
sol) (c)
=> 2 tan 30 deg
1 + (1)^2
=> 2tan 30 deg
2
=> tan 30 deg
*************************
(2) 1 - tan^2 45 deg
1 + tan^2 45 deg
(a) tan 90 deg
(b) 1
(c) sin 45 deg
(d) 0
sol) (d)
=> 1 - (1)^2
1 + (1)^2
=> 0
**********************
(3) 2 tan 30 deg
1 - tan^2 30 deg
(a) cos 60 deg
(b) sin 60 deg
(c) tan 60 deg
(d) sin 30 deg
sol) (C)
=> 2 * (1 / _/3)
-----------------------
1 - (1 / _/3)^2
=> 2 / _/3
----------
2 / 3
=> _/3
= tan 60 deg
************************
3) Evaluate sin 60 deg cos 30 deg + sin 30deg cos 60 deg. What is the value of sin( 60 deg + 30 deg). What can you conclude?
sol) Sin 60 deg Cos 30 deg + Sin 30 deg Cos 60 deg
*******************
sin 60 = _/3 / 2
Cos 30 = _/3 / 2
Sin 30 = 1 / 2
Cos 60 = 1 / 2
********************
Putting all values
Sin 60 deg Cos 30 deg + Sin 30 deg Cos 60 deg
=> ( _/3 /2) * ( _/3 / 2) + (1 / 2) * (1 / 2)
=> _/3 * _/3 + 1
-------------- ---------
2 * 2 2 * 2
=> 3 + 1
4 4
=> 3 + 1
4
1 = Sin 60 deg Cos 30 deg + Sin 30 deg Cos 60 deg
***********************************************
4) Is it right to say cos (60 deg + 30 deg) = cos 60 deg cos 30 deg - sin 60 deg sin 30 deg
sol) Yes, it is right to say
Proof :-
LHS :- Cos ( 60 + 30)
=> Cos ( 90)
=> 0
RHS :- Cos 60 Cos 30 - Sin 60 Sin 30
=> 1 / 2 * _/3 / 2 --- _/3 / 2 * 1 / 2
= 0
.^. cos (60 deg + 30 deg) = cos 60 deg cos 30 deg - sin 60 deg sin 30 deg
************************************************************
5) In right angle triangle /_\ PQR, right angle is at "Q" and PQ = 6 cm /_ RPQ = 60 deg . Determine the lengths of QR and PR.
sol) Given :- PQ = 6 cm and /_RPQ = 60 deg
Cos 60 = PQ
PR
1 = 6
2 PR
PR = 12 cm
Now,
QR^2 = (PR^2 -- PQ^2
QR^2 = (12)^2 --- ( 6)^2
QR^2 = 144 -- 36
QR^2 = 108
QR = _/ 36 * 3
QR = 6 _/3
.^. PR = 12 cm and QR = 6 _/3 cm
**********************************
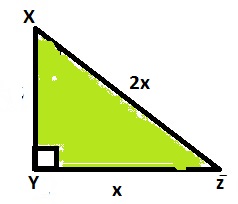
6) In /_\ XYZ , right angle is at Y, YZ = x , and XY = 2x then determine angle YXZ and angle YZX.
sol)
let /_YXZ = A
Sin A = YZ
XZ
=> X
2x
=> 1
2
Sin A = 1/2
***********************
We know, Sin 30 deg = 1/2
***********************
Sin 30 deg = 1 / 2
Hence
/_YXZ = 30 deg
.^. /_YZX = 60 deg [ Sum of angles of traingle is 180 ]
************************************************
7) Is it right to say that sin ( A + B ) = sin A + Sin B ? Justify your answer.
sol) Assume A = 30 and B = 60
LHS :- sin (A + B)
=> sin ( 30 + 60)
=> sin ( 90 )
=> 1
RHS :- sin 30 + sin 60
=> 1 / 2 + _/3 / 2
=> 1 + _/3
---------
2
LHS =/= RHS
Hence, it is not right to say
sin ( A + B ) = sin A + sin B is not true.
********************************************************************
(*) Trigonometric ratios of Complementary Angles
1) sin(90-x) = cos x
2) cos(90-x) = sin x
3) tan(90-x) = cot x
4) cot(90-x) = tan x
5) cosec(90-x) = sec x
6) sec(90-x) = cosec x
Example-8. Evaluate sec 35
cosec 55
sol) cosec A = sec(90-A)
cosec 55 = sec(90-35)
cosec 55 = sec 35
Now
sec 35 = sec 35 = 1
cosec 55 sec 35
*****************************************
Example-9. If cos 7A = sin(A-6), where 7A is an acute angle, find the value of A.
sol) Given cos 7A = sin(A - 6) ----(1)
sin(90-7A) = sin(A-6)
Since (90-7A) & (A-6) are both acute angles,
therefore
90 - 7A = A - 6
8A= 96
A = 12
*****************************************
Example-10. If sin A = cos B, then prove that A+B = 90
sol) Given that sin A = cos B -------(1)
we know
cos B= sin(90-B),
we can write (1) as
sin A = sin (90-B)
If A,B are acute angles,
then A = 90 - B
=> A + B = 90 deg
*****************************************
Example-11. Express sin 81 + tan 81 in terms of trigonometric ratios of angles between 0 deg and 45 deg.
sol) We can write
sin 81 = cosec(90-81) = cos 9
tan 81 = tan(90-81) = cot 9
Then,
sin 81 + tan 81 = cos 9 + cot 9
*****************************************
Example-12. if A,B and C are interior angles of triangle ABC, then show that
sin B+C = cos A
2 2
sol) Given A,B and C are interior angles of right angle triangle ABC then
A+B+C = 180 deg
On dividing the above equation by 2 on both sides, we get
A + B+C = 90 deg
2 2
B+C = 90 - A
2 2
On taking sin ratio on both sides
sin (B+C) = sin (90 - A)
2 2
sin ( B + C) = cos A
2 2
Hence proved
****************************************
Exercise 11.3
(1) Evaluate
(a) tan 36 deg
cos 54 deg
sol) We have => cot (90 -
Tan 36 deg = cot ( 90 - 36)
Tan 36 deg = cot (54)
Now,
Tan 36 = cot 54 = 1
Cot 54 cot 54
*****************************
(b) cos12 deg - sin78 deg
sol) We have => sin ( 90 -
(*) cos 12 - sin 78
=> sin ( 90 - 12) - sin 78
=> sin 78 -- sin 78 = 0
*******************************
(c) cosec31 deg - sec59 deg
sol) We have = > sec ( 90 -
=> sec (90 - 31) -- sec 59 deg
=> sec 91 - sec 91 = 0
********************************
(d) sin15 deg sec75 deg
sol) We have sin 15 = 1
cosec 15
=> 1
sec ( 90 - 15)
=> 1
sec 15
Now,
(*) sin 15 deg sec 75deg
=> 1
*************************
(c) tan26 deg tan64 deg
sol) We have cot (90 - 0) = tan
(*) tan 26deg tan 64deg
=> cot (90 - 26) tan 64
=> cot 64 tan 64
*********************/
We have=> cot
tan
*******************************
(2) Show that
1) tan48 deg tan16 deg tan42 deg tan74 deg = 1
sol) tan 48 * cot ( 90 - 16) * cot ( 90 - 42) * tan 74
=> tan 48 * cot 74 * cot 48 * tan 74
=>
Hence proved
************************************
2) cos36 deg cos54 deg - sin36 deg sin54 deg = 0
sol) cos 36 * sin ( 90 - 54) -- sin 36 * cos( 90 - 54)
=> (cos 36 * sin 36) -- ( sin 36 * cos 36)
=> 0
Hence proved.
*****************************************
(3) If tan 2A = cot( A - 18 deg), where 2A is an acute angle. Find the value of A.
sol) tan 2A = cot ( A- 18)
We have => cot ( 90 - 2A) = tan 2A
Now,
cot ( 90 - 2A) = cot ( A - 18)
comparing angles
90 - 2A = A - 18
90 + 18 = A + 2A
108 = 3A
108 = A
3
36 = A
.^. A = 36 deg
*************************************
(4) if tanA = cotB where A and B are acute angles, prove that A + B = 90 deg
sol) Given tan A = cot B
cot ( 90 - A) = cot B
90 - A = B
A+ B = 90
Thus proved
-************************
(5) If A, B and C are interior angles of triangle ABC , then show that tan ( A + B) = cot C
2 2
sol) Given A, B, and C are interior angles of a triangle ABC then A + B + C = 180 deg
Dividing the above equation by 2 on both sides, we get
A + B + C = 180
2 2
A + B + C = 90
2 2
A + B = 90 - C
2 2
Take "tan" ratio on both sides,
tan ( A + B ) = tan ( 90 - C )
2 2
We have = > tan ( 90 -
2 2
tan ( A + B ) = cot C
2 2
*********************************
(6) Express sin75 deg + cos65 deg in terms of trigonometric ratios of angles between 0deg and 45 deg.
sol) We can write
=> sin 75 = cos ( 90 - 75) = cos 15
=> cos 65 = sin ( 90 - 65 ) = sin 25
Then,
sin 75 + cos 65 = cos 15 + sin 25
15 and 25 are between 0 deg and 45 deg
*********************************************************************************
(*) Trigonometric Identities
We know that an identity is that mathematical equation which is true for all the value of the variable in the equation
Example:- (a+b)^2 = a^2 + b^2 + 2ab is an identity
In the same way, an identity equation having trigonometric ratios of an angle is called trigonometric identity .
1) sin^2 A + cos^2 A = 1
(Do not write cos A^2)
2) sec^2 A - tan^2 A = 1
*) 1 + tan^2 A = sec^2 A
3) cot^2 A + 1 = cosec^2 A
*) cosec^2 A - cot^2 A = 1
Example-13. Show that cot𝜽 + tan𝜽 = sec𝜽 cosec.
sol) LHS = cot𝜽 + tan𝜽
= cos𝜽 + sin𝜽
sin𝜽 cos𝜽
= cos^2𝜽 + sin^2𝜽
sin𝜽 cos𝜽
= 1
sin𝜽 cos𝜽
= 1 * 1
sin𝜽 cos𝜽
= cosec 𝜽 sec𝜽
*****************************************
Example-14. Show that tan^2𝜽 + tan^4𝜽 =sec^4𝜽 - sec^2𝜽
sol) L.H.S = tan^2𝜽 + tan^4𝜽
= tan^2𝜽(1 + tan^2𝜽)
= tan^2𝜽 . sec^2𝜽
= (Sec^2𝜽-1) . sec^2𝜽
= sec^4𝜽 - sec^2𝜽 = R.H.S
*****************************************
Example-15. Prove that
√1 + cos𝜽 = cosec𝜽 + cot𝜽
√1 - cos𝜽
sol) L.H.S = √1 +cos𝜽
√1 - cos𝜽
Multiply and divide by 1+cos 𝜽
= √1 + cos𝜽 . 1+ cos𝜽
√1 - cos𝜽 1+cos𝜽
= √(1 + cos𝜽)^2
√1 - cos^2𝜽
= √(1 + cos𝜽)^2
√sin^2𝜽
= 1 + cos𝜽
sin𝜽
= 1 + cos𝜽
sin𝜽 sin𝜽
= cosec𝜽 + cot = R.H.S
*****************************************
Exercise 11.4
(1) Evaluate the following :
(a) ( 1 + tan
sol) 1* ( 1 + cot
+ sec
=> ( 1 + cot
+ (sec
=> ( 1 + cot
sin
cos
-- sec
=> ( 1 + cot
=> 2 + cot
=> 2 + cos
sin
=> 2 + cos^2
cos
*****************************
=> 2 + 1 - 1
cos
=> 2
***************************************
(b) ( sin 0 + cos 0)^2 + ( sin
sol) it is in (a +b)^2 and (a-b)^2 form
=> (sin^2 0 + cos^2 0 + 2 sin
(sin^2 0 + cos^2 0
******************
sin^2
******************
=> (1 +
=> (1 + 1) = 2
*************************************
(c) ( sec^2
sol) sec^2
=> sec^2
=> 1 * 1 - ( 1 - 1 ) + 1
cos^2
=> 1 - cos^2
cos^2
= 1 - 1 + 1
cos^2
=> 0 + 1
=> 1
************************************
1 + cos
1 + cos
1 - cos
1 + cos
1^2 - cos^2
we have 1 - cos^2
*************************
sin^2
sin
=> [ 1 - cos 0]^2
sin
= LHS
************************************
1 - sin A
sol) LHS = _/ 1 + sin A
1- sin A
(multiply and divide by 1 + sin A )
= _/ 1 + sin A * 1 + sin A
1 - sin A 1 + sin A
= _/ ( 1 + sin A )^2
1^2 - sin^2A
(1 - sin^2A = cos^2 )
= 1 + sin A
cosA
= 1 + sin A
cos A cos A
= sec A + tan A = RHS
******************************
(4) Show that 1- tan^2 A = tan^2 A
cot^2 A - 1
sol) 1 - tan^2
cot^2A - 1
= 1 - tan^2
1 - 1
tan^2A
= 1 - tan^2
1 - tan^2A
tan^2A
= 1 - tan^2 A * tan^A
1 - tan^2A
=> tan^2A = RHS
******************************
(5) Show that 1 - cos
cos
cos
=> 1 -- cos^2
cos
=> sin^2
cos
=> sin 0 * sin
cos
**************************
sol) sec A ( secA + tanA -- sinA * 1 -- sinA tanA )
cosA
=> sec A ( secA + tanA - sinA -- sinA tanA )
cosA
=> sec A (secA +
=> sec A (secA -- sinA tanA )
=> sec^2 A -- 1 sinA tanA
cos A
=> sec^2A - sinA tanA
cosA
=> sec^2A -- tan^2A = 1
*********************************
(7) Prove that ( sinA + cosecA)^2 + (cosA + secA)^2 = 7 + tan^2A + cot^2A
sol) LHS = (sinA + cosecA)^2 + ( cosA + secA)^2
=> sin^2A + cosec^2A + 2sinA cosecA ) +
cos^A + 2 cosA secA + sec^2 A)
=> sin^2A + cosec^2A + 2sinA * 1 ) +
sinA
( cos^2A + sec^ A + 2cosA * 1 )
cos A
=> (sin^2A + 2 + cosec^2A) + ( cos^2A + 2 + sec^2A)
=> (sin^2A + cos^2A + 2 + 2 + cosec^2A + sec^2A)
=> ( 1 + 2 + 2 + cosec^2A + sec^2A)
*********************
cosec^2A = 1 + cot^2A
sec^2A = 1 + tan^2A
*********************
=> (5 + cot^2A + 1 + 1 +tan^2A)
=> (7 + cot^2A + tan^2A)
=> RHS
*****************************************
(8) Simply ( 1- cos
sol) ( 1 - cos
=> (1^2 -- cos^2
1 - cos^2
cosec^2
*******************
=> sin^2
sin^2
************************************
(9) If sec
sol) LHS = sec 0 + tan 0 = p
Multiply and dividing LHS by ( sec 0 - tan 0 )
Now,
(sec 0 + tan 0 ) ( sec 0 - tan 0) = p
sec 0 - tan 0
sec^2
sec 0 - tan
1 = p
sec 0 - tan
sec 0 - tan 0 = p
*******************************
(10) If cosec
k^2 + 1
sol) cosec
1 + cos
sin
1 + cos
sin
(1 + cos
sin^2
(1 + cos
1 -- cos^2
(1 + cos
(1-cos
1 + cos
1 + cos
cos
cos
k^2 + 1
hence proved
*********************************************************************************
(*) Optional Exercise
1) Prove that
cot𝜽 - cos𝜽 = cosec𝜽 - 1
cot𝜽 + cos𝜽 cosec𝜽 +1
sol) L.H.S = cot𝜽 - cos𝜽
cot𝜽 + cos𝜽
**********
cos𝜽 = cot𝜽
sin𝜽
**********
=> (cos𝜽 - cos𝜽)
sin𝜽
(cos𝜽 + cos𝜽)
sin𝜽
=>
sin𝜽
sin𝜽
****************
1 = cosec𝜽
sin𝜽
****************
=> cosec𝜽 - 1
cosec𝜽 +1
= R.H.S
*****************************************
2) Prove that
sin 𝜽 - cos𝜽 + 1 = 1
sin 𝜽 +cos𝜽 - 1 sec𝜽 - tan𝜽
using the identity sec^2𝜽 = 1 + tan^2𝜽
sol) L.H.S = (sin𝜽-cos𝜽+1)
(sin𝜽+cos𝜽-1)
divide Numerator and denominator by "cos𝜽"
= (sin𝜽-cos𝜽+1)
cos𝜽
(sin𝜽+cos𝜽-1)
cos𝜽
= ( sin𝜽 - cos𝜽 + 1 )
cos𝜽 cos𝜽 cos𝜽
(sin𝜽 +cos𝜽 - 1 )
cos𝜽 cos𝜽 cos𝜽
******************
we know
sin𝜽 = tan𝜽
cos𝜽
and
1 = sec𝜽
cos𝜽
******************
= (tan𝜽 - 1 + sec𝜽)
(tan𝜽 + 1- sec𝜽)
Multiply numerator and denominator by
(tan𝜽 - sec𝜽)
=(tan𝜽 - sec𝜽) * (tan𝜽 +sec𝜽 -1)
(tan𝜽 - sec𝜽) * (tan𝜽 -sec𝜽 +1)
= (tan^2𝜽 -sec^2𝜽) - (tan𝜽-sec𝜽)
(tan𝜽 - sec𝜽) + (tan𝜽 - sec𝜽+1)
= -(1 + tan𝜽 - sec𝜽)
(tan𝜽-sec𝜽)(tan𝜽 -sec𝜽+1)
= -1
tan𝜽-sec𝜽
= 1
sec𝜽-tan𝜽
= R.H.S
****************************************
3) Prove that
(cosecA-sinA)(secA-cosA) =
1
tanA + cotA
sol) L.H.S = (cosecA-sinA)(secA-cosA)
************
we know
1 = cosecA
sinA
1 = secA
cosA
******************
=( 1 - sinA) * ( 1 - cosA)
sinA cosA
= (1 - sin^2A) * ( 1 - cos^2A)
sinA cosA
**********************
we know
sin^2 A + cos^2 A = 1
1-sin^2 A = cos^2 A
or
1 - cos^2 A = sin^2 A
***********************
cos^2 A * ( sin^2 A)
= cos A * sin A
1
******************
in place of '1'
1 = sin^2 A + cos^2 A
*******************
= cos A * sin A
cos^2 A + sin^2 A
Divide numerator and denominator by
"cosA * sinA"
= cos A * sin A
cos A * sin A
=================
cos^2A + sin^2A
cosA * sinA
= 1
===============
cos^2 A + sin^2 A
cosA * sin A
= 1
=====================
(cos^2 A) + ( sin^2 A)
cosA*sinA cosA*sinA
= 1
===============
cos A + sin A
sin A cos A
= 1 = R.H.S
cot A + tan A
****************************************
*****************************************
4) Prove that
1 + secA = sin^2A
secA 1 - cosA
sol) L.H.S = 1 + sec A
sec A
**********
we know
1 = sec A
cos A
**********
= 1 + 1
cosA
==========
1
cos A
= cos A + 1
==========
1
= 1 + cos A
Multiply and divide by "1-cos A"
= 1 + cosA * 1 - cosA
1 - cosA
******************
we know
(1+cosA) * (1-cosA)
(a+b) (a-b) = a^2 - b^2
*************************
= 1 - cos^2A
1 - cosA
******************
we know
sin^2 A = 1 - cos^2 A
******************
= sin^2 A
1 - cos A
= R.H.S
*****************************************
5) Show that
( 1 +tan^2A) = (1 +tanA)^2 = tan^2A
(1 + cot^2 A) (1 - cotA)
sol) L.H.S = (1 + tan^2A)
(1 + cot^2A)
= 1 + sin^2 A
cos^2 A
============
1 + cos^2 A
sin^2 A
= cos^2 A + sin^2 A
cos^2 A
===============
sin^2 A + cos^2 A
sin^2 A
= 1
cos^2 A
======
1
sin^2 A
= 1 * sin^2 A
cos^2 A 1
= sin^2 A
cos^2 A
= tan^2 A
******************
(!!) L.H.S = ( 1 - tanA)^2
( 1 - cotA)^2
sol) Its in form of
(a-b)^2 = (1-tanA)^2
(a-b)^2 = (1 - cotA)^2
expand we get,
= (1 +tan^2 A - 2tan A)
(1 +cot^2 A - 2cot A)
****************
we know
sec^2 A = 1 + tan^2 A
and
cosec^2 A = 1 + cot^2 A
*********************
= (sec^2 A - 2tan A)
(cosec^2 A - 2 cot A)
= sec^2 A - 2 * sin A
cos A
================
cosec^2 A - 2 * cos A
sin A
= 1 - 2 * sin A
cos^2 A cos A
================
1 - 2 * cos A
sin^2 A sin A
cos^2 A
==================
sin^2 A
= sin^2 A
cos^2 A
= tan^2 A = R.H.S
****************************************
6) Prove that
(secA-1) = (1-cosA)
(secA+1) (1+cosA)
sol) L.H.S = (sec A - 1 )
(sec A + 1)
***************
we know
1 = sec A
cos A
**************
Now
= ( 1 - 1 )
cos A
============
( 1 + 1 )
cos A
= (1 - cos A)
=========
(1 + cos A)
= ( 1 - cos A) = R.H.S
( 1 + cos A)
******************************************














No comments:
Post a Comment